定义在R上的函数y=f(x)满足下列两个条件:(1)对于任意的0≤x1<x2≤2,都有f(x1)<f(x2);(2)y=f(x+2)的图象关于y轴对称.则下列结论中,正确的是( )| A.f()<f()<f(3) | B.f()<f(3)<f() | C.f(7)<f()<f() | D.f(7)<f()<f() |
|
相关习题
科目:高中数学
来源:
题型:
定义在R上的函数y=f(x)满足下列两个条件:(1)对于任意的0≤x1<x2≤2,都有f(x1)<f(x2);(2)y=f(x+2)的图象关于y轴对称.则下列结论中,正确的是( )
| | | |
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
定义在R上的函数y=f(x)满足下列两个条件:(1)对于任意的0≤x
1<x
2≤2,都有f(x
1)<f(x
2);(2)y=f(x+2)的图象关于y轴对称.则下列结论中,正确的是( )
| A.f()<f()<f(3) | B.f()<f(3)<f() | C.f(7)<f()<f() | D.f(7)<f()<f() |
查看答案和解析>>
科目:高中数学
来源:2011-2012学年吉林省松原市前郭五中高一(上)月考数学试卷(解析版)
题型:选择题
定义在R上的函数y=f(x)满足下列两个条件:(1)对于任意的0≤x
1<x
2≤2,都有f(x
1)<f(x
2);(2)y=f(x+2)的图象关于y轴对称.则下列结论中,正确的是( )
A.

B.

C.

D.

查看答案和解析>>
科目:高中数学
来源:2009-2010学年重庆一中高一(上)期中数学试卷(解析版)
题型:选择题
定义在R上的函数y=f(x)满足下列两个条件:(1)对于任意的0≤x
1<x
2≤2,都有f(x
1)<f(x
2);(2)y=f(x+2)的图象关于y轴对称.则下列结论中,正确的是( )
A.
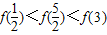
B.
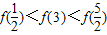
C.

D.

查看答案和解析>>
科目:高中数学
来源:
题型:单选题
定义在R上的函数y=f(x)满足下列两个条件:(1)对于任意的0≤x1<x2≤2,都有f(x1)<f(x2);(2)y=f(x+2)的图象关于y轴对称.则下列结论中,正确的是
- A.
- B.
- C.
- D.
查看答案和解析>>
科目:高中数学
来源:
题型:
给出下列函数:①y=x
2+1;②y=-|x|;③y=(
)
x;④y=log
2x;
其中同时满足下列两个条件的函数的个数是( )
条件一:定义在R上的偶函数;
条件二:对任意x
1,x
2∈(0,+∞),(x
1≠x
2),有
<0.
查看答案和解析>>
科目:高中数学
来源:2012-2013学年安徽省六安市寿县二中高三(上)月考数学试卷(解析版)
题型:填空题
给出下列六个命题:
①函数f(x)=lnx-2+x在区间(1,e)上存在零点;
②若f′(x
)=0,则函数y=f(x)在x=x
处取得极值;
③若m≥-1,则函数y=

的值域为R;
④“a=1”是“函数

在定义域上是奇函数”的充分不必要条件.
⑤函数y=f(1+x)的图象与函数y=f(l-x)的图象关于y轴对称;
⑥满足条件AC=

,AB=1的三角形△ABC有两个.
其中正确命题的个数是
.
查看答案和解析>>
科目:高中数学
来源:2012-2013学年吉林省松原市油田高中高三(上)第二次摸底数学试卷(理科)(解析版)
题型:填空题
给出下列六个命题:
①函数f(x)=lnx-2+x在区间(1,e)上存在零点;
②若f′(x
)=0,则函数y=f(x)在x=x
处取得极值;
③若m≥-1,则函数y=
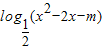
的值域为R;
④“a=1”是“函数
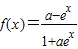
在定义域上是奇函数”的充分不必要条件.
⑤函数y=f(1+x)的图象与函数y=f(l-x)的图象关于y轴对称;
⑥满足条件AC=
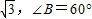
,AB=1的三角形△ABC有两个.
其中正确命题的个数是
.
查看答案和解析>>
科目:高中数学
来源:2012-2013学年吉林省松原市油田高中高三(上)第二次摸底数学试卷(文科)(解析版)
题型:填空题
给出下列六个命题:
①函数f(x)=lnx-2+x在区间(1,e)上存在零点;
②若f′(x
)=0,则函数y=f(x)在x=x
处取得极值;
③若m≥-1,则函数y=

的值域为R;
④“a=1”是“函数

在定义域上是奇函数”的充分不必要条件.
⑤函数y=f(1+x)的图象与函数y=f(l-x)的图象关于y轴对称;
⑥满足条件AC=

,AB=1的三角形△ABC有两个.
其中正确命题的个数是
.
查看答案和解析>>
科目:高中数学
来源:2012-2013学年安徽省六安市寿县二中高三(上)月考数学试卷(解析版)
题型:填空题
给出下列六个命题:
①函数f(x)=lnx-2+x在区间(1,e)上存在零点;
②若f′(x
)=0,则函数y=f(x)在x=x
处取得极值;
③若m≥-1,则函数y=
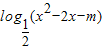
的值域为R;
④“a=1”是“函数
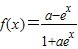
在定义域上是奇函数”的充分不必要条件.
⑤函数y=f(1+x)的图象与函数y=f(l-x)的图象关于y轴对称;
⑥满足条件AC=
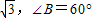
,AB=1的三角形△ABC有两个.
其中正确命题的个数是
.
查看答案和解析>>





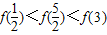
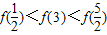


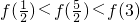
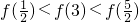
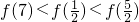
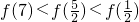
 的值域为R;
的值域为R; 在定义域上是奇函数”的充分不必要条件.
在定义域上是奇函数”的充分不必要条件. ,AB=1的三角形△ABC有两个.
,AB=1的三角形△ABC有两个.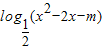 的值域为R;
的值域为R;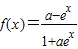 在定义域上是奇函数”的充分不必要条件.
在定义域上是奇函数”的充分不必要条件.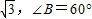 ,AB=1的三角形△ABC有两个.
,AB=1的三角形△ABC有两个. 的值域为R;
的值域为R; 在定义域上是奇函数”的充分不必要条件.
在定义域上是奇函数”的充分不必要条件. ,AB=1的三角形△ABC有两个.
,AB=1的三角形△ABC有两个.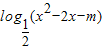 的值域为R;
的值域为R;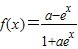 在定义域上是奇函数”的充分不必要条件.
在定义域上是奇函数”的充分不必要条件.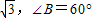 ,AB=1的三角形△ABC有两个.
,AB=1的三角形△ABC有两个.