| 已知函数y=f(x)=ax+k经过点(0,4),其反函数y=f-1(x)的图象经过点(7,1),则f(x)在定义域上是( ) |
相关习题
科目:高中数学
来源:
题型:
已知函数y=f(x)=ax+k经过点(0,4),其反函数y=f-1(x)的图象经过点(7,1),则f(x)在定义域上是( )
查看答案和解析>>
科目:高中数学
来源:2009-2010学年河南省信阳市息县高中高三(上)开学数学试卷(文科)(解析版)
题型:选择题
已知函数y=f(x)=ax+k经过点(0,4),其反函数y=f-1(x)的图象经过点(7,1),则f(x)在定义域上是( )
A.奇函数
B.偶函数
C.增函数
D.减函数
查看答案和解析>>
科目:高中数学
来源:2011年江西师大附中高考数学模拟试卷(文科)(解析版)
题型:选择题
已知函数y=f(x)=ax+k经过点(0,4),其反函数y=f-1(x)的图象经过点(7,1),则f(x)在定义域上是( )
A.奇函数
B.偶函数
C.增函数
D.减函数
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
已知函数y=f(x)=a
x+k经过点(0,4),其反函数y=f
-1(x)的图象经过点(7,1),则f(x)在定义域上是( )
查看答案和解析>>
科目:高中数学
来源:
题型:单选题
已知函数y=f(x)=ax+k经过点(0,4),其反函数y=f-1(x)的图象经过点(7,1),则f(x)在定义域上是
- A.
奇函数
- B.
偶函数
- C.
增函数
- D.
减函数
查看答案和解析>>
科目:高中数学
来源:2012-2013学年山东省潍坊市奎文一中高三(上)12月月考数学试卷(文科)(解析版)
题型:填空题
给出以下五个命题:
①命题“?x∈R,x
2+x+1>0”的否定是:“?x∈R,x
2+x+1<0”.
②已知函数f(x)=k•cosx的图象经过点P(
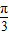
,1),则函数图象上过点P的切线斜率等于

③a=1是直线y=ax+1和直线y=(a-2)x-1垂直的充要条件.
④函数

在区间(0,1)上存在零点.
⑤已知向量

与向量

的夹角为锐角,那么实数m的取值范围是(

)
其中正确命题的序号是
.
查看答案和解析>>
科目:高中数学
来源:2013学年安徽省芜湖市高考数学二模试卷(文科)(解析版)
题型:填空题
给出以下五个命题:
①命题“?x∈R,x
2+x+1>0”的否定是:“?x∈R,x
2+x+1<0”.
②已知函数f(x)=k•cosx的图象经过点P(
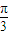
,1),则函数图象上过点P的切线斜率等于
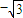
③a=1是直线y=ax+1和直线y=(a-2)x-1垂直的充要条件.
④函数
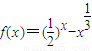
在区间(0,1)上存在零点.
⑤已知向量
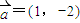
与向量
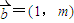
的夹角为锐角,那么实数m的取值范围是(
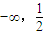
)
其中正确命题的序号是
.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
已知函数f(x)=ex(ax+b),曲线y=f(x)经过点P(0,2),且在点P处的切线为l:y=4x+2.
(1)求常数a,b的值;
(2)求证:曲线y=f(x)和直线l只有一个公共点;
(3)是否存在常数k,使得x∈[-2,-1],f(x)≥k(4x+2)恒成立?若存在,求常数k的取值范围;若不存在,简要说明理由.
查看答案和解析>>
科目:高中数学
来源:
题型:
(2014•江门模拟)已知函数f(x)=ex(ax+b),曲线y=f(x)经过点P(0,2),且在点P处的切线为l:y=4x+2.
(1)求常数a,b的值;
(2)求证:曲线y=f(x)和直线l只有一个公共点;
(3)是否存在常数k,使得x∈[-2,-1],f(x)≥k(4x+2)恒成立?若存在,求常数k的取值范围;若不存在,简要说明理由.
查看答案和解析>>
科目:高中数学
来源:芜湖二模
题型:填空题
给出以下五个命题:
①命题“?x∈R,x
2+x+1>0”的否定是:“?x∈R,x
2+x+1<0”.
②已知函数f(x)=k•cosx的图象经过点P(
,1),则函数图象上过点P的切线斜率等于
-③a=1是直线y=ax+1和直线y=(a-2)x-1垂直的充要条件.
④函数
f(x)=()x-x在区间(0,1)上存在零点.
⑤已知向量
=(1,-2)与向量
=(1,m)的夹角为锐角,那么实数m的取值范围是(
-∞,)
其中正确命题的序号是______.
查看答案和解析>>

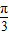 ,1),则函数图象上过点P的切线斜率等于
,1),则函数图象上过点P的切线斜率等于
 在区间(0,1)上存在零点.
在区间(0,1)上存在零点. 与向量
与向量 的夹角为锐角,那么实数m的取值范围是(
的夹角为锐角,那么实数m的取值范围是( )
)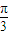 ,1),则函数图象上过点P的切线斜率等于
,1),则函数图象上过点P的切线斜率等于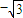
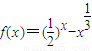 在区间(0,1)上存在零点.
在区间(0,1)上存在零点.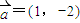 与向量
与向量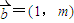 的夹角为锐角,那么实数m的取值范围是(
的夹角为锐角,那么实数m的取值范围是(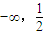 )
)