
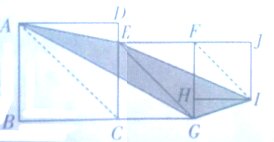
 四边形ABCD、CEFG、HFJI都是正方形,边长分别是5厘米,4厘米,3厘米,你能求出下图中阴影部分的面积吗?(提示:下图中三条对角线AC、EG、FI是互相平行的,分别找出与三角形AEG、三角形EGI面积相等的三角形即可)
四边形ABCD、CEFG、HFJI都是正方形,边长分别是5厘米,4厘米,3厘米,你能求出下图中阴影部分的面积吗?(提示:下图中三条对角线AC、EG、FI是互相平行的,分别找出与三角形AEG、三角形EGI面积相等的三角形即可) 分析 因为AC∥EG,所以△AEG与△GEC当底边为EG时,它们的高相等,即△AEG的面积=△GEC的面积=正方形EFGC的面积的$\frac{1}{2}$;同理可得:△EGI的面积=△EGF的面积=正方形EFGC的面积的$\frac{1}{2}$;阴影部分的面积=△AEG的面积+△EGI的面积=正方形CEFG的面积;据此解答即可.
解答 解:因为AC∥EG,所以△AEG与△GEC当底边为EG时,它们的高相等,即△AEG的面积=△GEC的面积=正方形EFGC的面积的$\frac{1}{2}$;
同理可得:△EGI的面积=△EGF的面积=正方形EFGC的面积的$\frac{1}{2}$;
阴影部分的面积=△AEG的面积+△EGI的面积=正方形CEFG的面积=4×4=16(平方厘米)
答:阴影部分的面积是16平方厘米.
点评 解答本题的关键是利用等积转换,即等底等高的三角形面积相等,将阴影部分重组,从而利用已知条件求得阴影部分的面积.


科目:小学数学 来源: 题型:解答题
查看答案和解析>>
科目:小学数学 来源: 题型:填空题
| 6÷8=$\frac{6}{8}$(或$\frac{3}{4}$) | 7÷10=$\frac{7}{10}$ | 3÷4=$\frac{3}{4}$ |
| 8÷11=$\frac{8}{11}$ | 19÷24=$\frac{19}{24}$ | 5÷7=$\frac{5}{7}$ |
查看答案和解析>>
科目:小学数学 来源: 题型:解答题
 附加题:一个正方体的底面不变,高增加4cm,便得到一个长方体,这个长方体的表面积比原来正方体的表面积增加96cm3,原来的正方体的体积是多少立方厘米?
附加题:一个正方体的底面不变,高增加4cm,便得到一个长方体,这个长方体的表面积比原来正方体的表面积增加96cm3,原来的正方体的体积是多少立方厘米?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com