
| A. | 等于圆锥的高 | B. | 等于圆锥的高的$\frac{1}{3}$ | ||
| C. | 等于圆锥的高的3倍 |
分析 圆锥的体积=$\frac{1}{3}$×底面积×高,圆柱的体积=底面积×高,这块铁的体积是不变的,即圆锥的体积等于圆柱的体积,设底面积相等为s,圆锥体的高为h锥,圆柱体的高为h柱,代入公式即可求出圆柱体的高和圆锥体的高关系即可.
解答 解:设圆锥体的高为h锥,圆柱体的高为h柱,底面积为S,则圆柱的底面积也为S,体积设为V,
则:Sh柱=$\frac{1}{3}$×S×h锥
h柱=$\frac{1}{3}$h锥
即,圆柱的高等于圆锥的高的$\frac{1}{3}$.
故选:B.
点评 此题主要考查圆锥与圆柱体的体积公式的灵活应用,知识点:圆柱的体积=底面积×高,用字母表示:V=Sh=πr2h;圆锥的体积=$\frac{1}{3}$×底面积×高,用字母表示:V=$\frac{1}{3}$Sh=$\frac{1}{3}$πr2h,(S表示底面积,h表示高).


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案科目:小学数学 来源: 题型:操作题
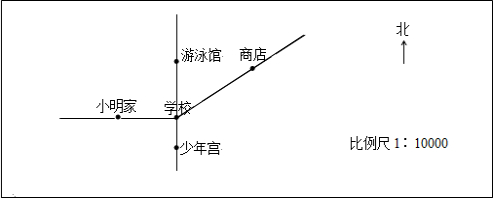
查看答案和解析>>
科目:小学数学 来源: 题型:计算题
| $\frac{3}{5}$×$\frac{1}{2}$+$\frac{1}{2}$×$\frac{2}{5}$ | $\frac{1}{4}$×$\frac{8}{15}$÷$\frac{2}{5}$ | $\frac{7}{9}$÷$\frac{11}{5}$+$\frac{2}{9}$×$\frac{5}{11}$ |
| $\frac{3}{7}$×$\frac{1}{6}$+$\frac{3}{7}$ | 368÷[1÷(2.1-2.09)] | $\frac{7}{10}$×99+$\frac{7}{10}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com