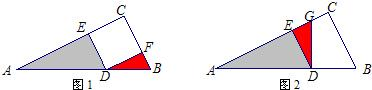
解:活动一:
因为四边形DECF是正方形,
所以DE=DF=x,DE∥BC,DF∥AC,
所以

=

,
=

,
因为AD=2,BD=1,
所以AC=3x,BC=

x,
因为AC
2+BC
2=AB
2,
所以9x
2+(

x)
2=9,
解得:x=

,
所以DE=DF=

,AE=


,BF=

,
所以S
△ADE+S
△BDF=1,
所以S
阴影=1;
故答案为:1;
活动二:根据题意得:∠EAG=90°,
因为AE⊥BC,
所以∠AEB=∠AEC=∠G=90°,
所以四边形AECG是矩形,
因为AE=AG,
所以四边形AECG是正方形,
因为BC=5,CD=3,
所以设AE=x,则BE=GD=CG-CD=x-3,
BE=BC-EC=5-x,
所以x-3=5-x,
解得:x=4,
所以AE=4.
故答案为:正方形;4.
活动三:
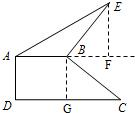
过点B作BG⊥DC于点G,过点E作EF⊥AB与AB的延长线交于点F.
因为∠BAD=∠D=∠DGB=90°,
所以四边形ABGD是矩形,
所以DG=AB=2,
所以CG=DC-DG=4-2=2.
因为∠CBG+∠CBF=90°,∠EBF+∠CBF=90°,
所以∠CBG=∠EBF.
在△BCG与△BEF中,∠CBG=∠EBF,∠CGB=∠EFB=90°,BC=BE,
所以△BCG≌△BEF,
所以CG=EF=2.
所以S
△ABE=

AB?EF=2.
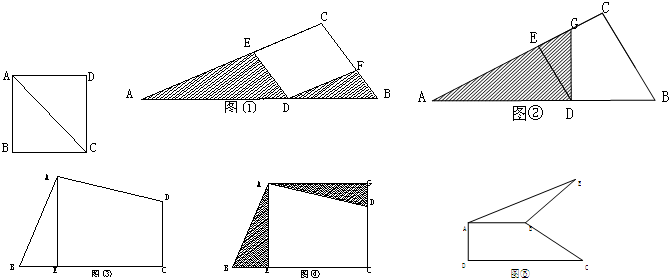
分析:(1)根据旋转的性质可知△DBF≌△DGE,则DG=BD=1,那么阴影部分的面积=Rt△ADG的面积=

×AD×DG;
(2)根据旋转的性质可知△ABE≌△ADG,得出∠AEB=∠G=90°,BE=DG,AE=AD.在四边形AECD中,有∠AEC=∠C=∠G=90°,则四边形AECD是矩形,又AE=AD,则矩形AECD是正方形;设BE=x,则DG=x,EC=CG=DG+CD=x+3,BC=BE+EC=x+x+3=5,求出x,进而得出AE的长;
(3)过点B作BG⊥DC于点G,过点E作EF⊥AB与AB的延长线交于点F,通过证明△BCG≌△BEF,从而得出S
△ABE的值.
点评:本题主要考查了旋转变换及其性质.在解题中进行旋转变换的目的在于通过旋转变换可以使图形发生重组,使分散的条件得以集中,然后运用旋转的“不变性”可以使一些问题迎刃而解.一般来说,当图形中有“共点等边”的图形时,常进行旋转变换.


 解:活动一:
解:活动一: =
= ,
, =
= ,
, x,
x, x)2=9,
x)2=9, ,
, ,AE=
,AE=
 ,BF=
,BF= ,
, 过点B作BG⊥DC于点G,过点E作EF⊥AB与AB的延长线交于点F.
过点B作BG⊥DC于点G,过点E作EF⊥AB与AB的延长线交于点F. AB?EF=2.
AB?EF=2. ×AD×DG;
×AD×DG;

 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案