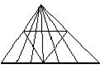
考点:组合图形的计数
专题:几何的计算与计数专题
分析:观察图形可知,(1)以A为顶点,以最下边横着的边为底的三角形有:6+5+4+3+2+1=21个;以中间横着的边为底的三角形也有21个;以斜线为底的三角形有(3+2+1)×2=12个;
(2)以B和D为顶点的有:3+3+1=7个,
(3)以点C为顶点的(除去重合的)有3+3=6个;由此即可解决问题.
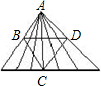
解答:
解:根据题干分析可得,
图中的三角形一共有
(6+5+4+3+2+1)×2+(3+2+1)×2+(3+3+1)+(3+3)
=21×2+6×2+7+6
=42+12+7+6
=67(个).
答:共有67个不同的三角形.
故答案为:67.
点评:此题主要考查了计数方法的应用,根据不同的顶点分别列举得出是解题的关键.