
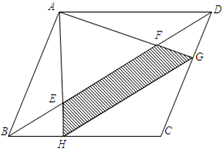
 如图,平行四边形ABCD的面积为36平方厘米,H、G分别是 BC、CD边上靠近B和D的三等分点,四边形EFGH的面积为________平方厘米.
如图,平行四边形ABCD的面积为36平方厘米,H、G分别是 BC、CD边上靠近B和D的三等分点,四边形EFGH的面积为________平方厘米. S平行四边形ABCD,于是可以求得这四个三角形的面积,并能得出S△AHC=S△AGC,从而可以得出E、F、O为BD的4等分点,则可以求出三角形AEF的面积=
S平行四边形ABCD,于是可以求得这四个三角形的面积,并能得出S△AHC=S△AGC,从而可以得出E、F、O为BD的4等分点,则可以求出三角形AEF的面积= ×
× S平行四边形ABCD,又因三角形HCG与三角形BCD是相似三角形,且相似比为2:3,则其面积比为4:9,从而可以求出三角形HCG的面积,阴影部分的面积=S△AHC+S△AGC-S△AEF-S△HCG,从而可以求出阴影部分的面积.
S平行四边形ABCD,又因三角形HCG与三角形BCD是相似三角形,且相似比为2:3,则其面积比为4:9,从而可以求出三角形HCG的面积,阴影部分的面积=S△AHC+S△AGC-S△AEF-S△HCG,从而可以求出阴影部分的面积.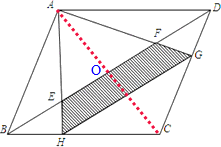
 S平行四边形ABCD=
S平行四边形ABCD= ×36=18(平方厘米),
×36=18(平方厘米), ×18=12(平方厘米),
×18=12(平方厘米), ×
× S平行四边形ABCD=
S平行四边形ABCD= ×36=9(平方厘米),
×36=9(平方厘米), S△BCD=
S△BCD= ×18=(平方厘米),
×18=(平方厘米),

科目:小学数学 来源: 题型:
 如图,平行四边形ABCD的一边AB=8厘米,AB上的高等于3厘米,四边形EFOG的面积等于2平方厘米,则阴影部分的面积与平行四边形的面积之比是
如图,平行四边形ABCD的一边AB=8厘米,AB上的高等于3厘米,四边形EFOG的面积等于2平方厘米,则阴影部分的面积与平行四边形的面积之比是查看答案和解析>>
科目:小学数学 来源: 题型:
 如图,平行四边形ABCD,△EBA是直角三角形,AB=80cm,EB=70cm.已知阴影部分的面积比三角形EFH的面积大120cm2.求HB的长度.
如图,平行四边形ABCD,△EBA是直角三角形,AB=80cm,EB=70cm.已知阴影部分的面积比三角形EFH的面积大120cm2.求HB的长度.查看答案和解析>>
科目:小学数学 来源: 题型:
 (2010?邯山区)已知如图,平行四边形ABCD的边AB是半圆O的直径,边AB 的中点O是半圆的圆心,且半圆O的圆周经过点D,DO与AB垂直,垂足是点O,AB=6.求图中阴影部分的面积.
(2010?邯山区)已知如图,平行四边形ABCD的边AB是半圆O的直径,边AB 的中点O是半圆的圆心,且半圆O的圆周经过点D,DO与AB垂直,垂足是点O,AB=6.求图中阴影部分的面积.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com