解:(1)(40-12)÷(3-1)-12,
=28÷2-12,
=14-12,
=2(年);
答:2年后小红的年龄是爸爸年龄的

.
(2)因为,三个质数的和是80,
所以,而必有一个是偶数,
而既是偶数又是质数的只有2,
所以三个数之中的一个是2,
另两个的和为78.
要使乘积的最大,
则另两个数很接近,接近78÷2=39,
质数为37,41;
所以这三个数为 2,37,41;
(3)
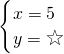
+(n-1)×
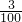
=

,
2+3n-3=98,
3n=99,
n=99÷3,
n=33;
(4)长是:(8÷2)=4(份),
设一份是a厘米,
则4a×3a=12a
2,
即12a
2=192,
a
2=192÷12,
a
2=16,
所以,a=4,
长方形的长是4×4=16(厘米),
宽是:4×3=12(厘米),
周长是(16+12)×2,
=28×2,
=56(厘米);
答:这个长方形的周长是56厘米.
故答案为:2;2,37,41,33;56.
分析:(1)先求出小红与爸爸的年龄差,再根据“小红的年龄是爸爸年龄的

,”知道爸爸的年龄是小红的3倍,由此根据差倍公式,列式即可求出几年后小红的年龄,进而求出要求的答案;
(2)三个质数的和是80,故而必有一个是偶数,而既是偶数又是质数的只有2,所以三个数之中的一个是2,另两个的和为78;要使乘积的最大,则另两个数很接近,接近78÷2=39,质数为37,41;由此得出答案;
(3)观察给出的数列,知道此数列是一个公差为
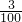
,首项为
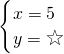
,的等差数列,根据等差数列的通项公式,a
n=a
1+(n-1)×d,即可求出项数;
(4)根据“一个等腰三角形底和高的比是8:3,”知道等腰三角形的底的一半与高的比是(8÷2):3,所拼成的长方形的长与宽的比是(8÷2):3,由此把长方形的长看作(8÷2)份,宽看作3份,再根据长方形的面积是192平方厘米,求出一份,进而求出长方形的面积.
点评:解答此题的关键是根据各个题目的要求,找出其中的数量关系或规律,利用相应的公式解决问题.

 .
.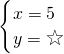 、
、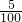 、
、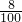 、
、 、…那么
、…那么 在这列数中的第______个数.
在这列数中的第______个数. .
.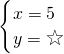 +(n-1)×
+(n-1)×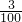 =
= ,
, ,”知道爸爸的年龄是小红的3倍,由此根据差倍公式,列式即可求出几年后小红的年龄,进而求出要求的答案;
,”知道爸爸的年龄是小红的3倍,由此根据差倍公式,列式即可求出几年后小红的年龄,进而求出要求的答案;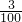 ,首项为
,首项为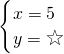 ,的等差数列,根据等差数列的通项公式,an=a1+(n-1)×d,即可求出项数;
,的等差数列,根据等差数列的通项公式,an=a1+(n-1)×d,即可求出项数;
