
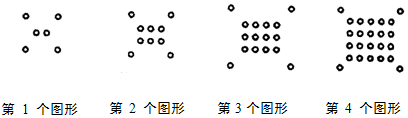
分析 观察图形发现:
第一个图中间有1行,每行的个数是1+1,
第2个图中间有2行,每行的个数是2+1,
第3个图中间有3行,每行的个数是3+1,
第4个图中间有4行,每行的个数是4+1,
所以,第一个图的个数是:1个2加上4,1×2+4=6个,
第二个图的个数是:2个3加上4,2×3+4=10个,
第三个图的个数是:3个4加上4,3×4+4=16个,
第一个图的个数是:4个5加上4,4×5+4=24个,
规律是:第几个图形的个数就等于几乘(几+1)加4.
据此解答即可.
解答 解:由分析可得,规律是:第几个图形的个数就等于几个(几+1)的积加上4.
所以,第n个图形的个数是:n(n+1)+4.
故答案为:n(n+1)+4.
点评 本题考查了数与形结合的规律,要认真观察数形的排列规律,找出规律,再利用规律解决问题.


科目:小学数学 来源: 题型:解答题
| 分数 | 100分 | 99~90分 | 89~80分 | 79~70分 | 69~60分 | 60分以下 |
| 人数 |
查看答案和解析>>
科目:小学数学 来源: 题型:解答题
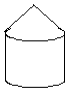 一个稻谷囤上面是圆锥形,下面是圆柱形(如图所示)圆柱的底面周长9.42m,高2m;圆锥的高是0.4m.如果每立方米的稻谷重550kg,这囤稻谷重多少千克?
一个稻谷囤上面是圆锥形,下面是圆柱形(如图所示)圆柱的底面周长9.42m,高2m;圆锥的高是0.4m.如果每立方米的稻谷重550kg,这囤稻谷重多少千克?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com