
分析 (1)分子依次是1,3,5,7…分子依次增加2;
分母依次是2,4,8,16后一个数是前一个数的2倍,由此求解.
(2)观察发现,每组数中的两个数互为倒数,由此求解.
解答 解:(1)要求数的分子依次是:7+2=9,9+2=11,
分母依次是:16×2=32,32×2=64;
所以要求的数就是:$\frac{9}{32}$,$\frac{11}{64}$.
(2)8与$\frac{1}{8}$互为倒数,所以这组数是(8,$\frac{1}{8}$)
16与$\frac{1}{16}$互为倒数,所以这组数是(16,$\frac{1}{16}$)
故答案为:$\frac{9}{32}$,$\frac{11}{64}$;$\frac{1}{8}$,$\frac{1}{16}$.
点评 关键是根据已知的数得出前后数之间的变化关系的规律,然后再利用这个变化规律再回到问题中去解决问题.


科目:小学数学 来源: 题型:填空题
查看答案和解析>>
科目:小学数学 来源: 题型:填空题
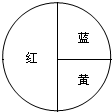 看图回答问题
看图回答问题查看答案和解析>>
科目:小学数学 来源: 题型:选择题
| A. | 成反比例 | B. | 成正比例 | C. | 不成比例 |
查看答案和解析>>
科目:小学数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com