
 直线1上最多能找到________个点,使它与A、B一起组成等腰三角形的三个顶点.
直线1上最多能找到________个点,使它与A、B一起组成等腰三角形的三个顶点.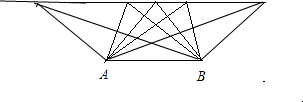


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:小学数学 来源:同步题 题型:解答题
| (1)小静在圆形纸片上作直线,发现一条直线可以把纸片分成两部分(大小不限),那么两条直线最多能把圆形纸片分成几部分呢?3条呢?先画一下 试试看,找到规律后,算一算,如果在圆形纸片上画100条直线,最多能把 它分成多少部分呢?(下表为发现的规律) | ||||||||||||||
| ||||||||||||||
| (2)在12×12 =144个方格中画一条直线,这条直线最多可穿过多少个方格? 试试看。 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com