练习册

  • 练习册
  • 试题
    精英家教网 > 小学数学 > 题目详情
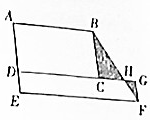
    14．如图，ABCD是长6厘米，宽3厘米的长方形，DEFG是长10厘米，宽1厘米的长方形，那么三角形BCH与三角形FGH的面积之差为多少？

    分析 如图，延长BC至I，交EF于I，要求三角形BCH与三角形FGH的面积之差，就是求三角形BIF与长方形CIFG之差，根据三角形和长方形面积公式解答即可．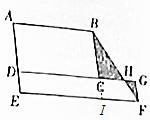

    解答 解：（10-6）×（3+1）÷2-（10-6）×1
    =4×4÷2-4
    =8-4
    =4（平方厘米）
    答：三角形BCH与三角形FGH的面积之差为4平方厘米．

    点评 此题解答的关键在于把图形面积进行转化，把求三角形BCH与三角形FGH的面积之差转换成求三角形BIF与长方形CIFG之差．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：小学数学 来源： 题型：解答题

    4．用2、4、6、8可以组成多少个没有重复数字的三位数？

    查看答案和解析>>

    科目：小学数学 来源： 题型：填空题

    5．如果x÷y=$\frac{7}{10}$，那么x一定是7，y一定是10．×．（判断对错）

    查看答案和解析>>

    科目：小学数学 来源： 题型：解答题

    2．解方程．
    （1）$\frac{17}{24}$x=$\frac{5}{12}$            
    （2）x：$\frac{8}{21}$=42：36         
    （3）80%x-$\frac{3}{5}$=$\frac{7}{5}$            
    （4）35%x+40%x=120．

    查看答案和解析>>

    科目：小学数学 来源： 题型：填空题

    9．东东每13天去公园一次，涛涛每15天去去公园一公园一次，今年东东3月30日曾去公园，涛涛4月1日曾去公园，以后他们在这公园第一次相遇的日期将是9月28日．

    查看答案和解析>>

    科目：小学数学 来源： 题型：解答题

    19．把一张长方形纸片按如图所示方法剪开后，正好可以做成一个圆柱，做成的圆柱的底面直径和底面周长分别是多少？

    查看答案和解析>>

    科目：小学数学 来源： 题型：填空题

    6．如图，有两个同样的圆柱形水杯，把两个同样的瓷球放在同一杯中，将另一个满杯的水倒入装有瓷球的杯中，将其倒满，此时杯中还剩有150毫升的水，每个瓷球的体积是75立方厘米．

    查看答案和解析>>

    科目：小学数学 来源： 题型：解答题

    3．小青买4节五号电池，付出10元，找回1.6元，每节五号电池的价格是多少元？（列方程并写出关系式）

    查看答案和解析>>

    科目：小学数学 来源： 题型：填空题

    13．公共汽车上原有48人，到A站下去b人，又上来c人，现在车上有（48-b+c）人；
    超市一天上午卖出40盒酸奶，每盒酸奶卖t元，一共买40t元．

    查看答案和解析>>

    同步练习册答案