
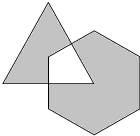
 如图所示,正三角形的一个顶点在正六边形的中心,且正六边形的面积是3cm2,正三角形的面积是2cm2,求阴影部分的面积.
如图所示,正三角形的一个顶点在正六边形的中心,且正六边形的面积是3cm2,正三角形的面积是2cm2,求阴影部分的面积. 分析 如图,根据正六边形的中心到各顶点的距离相等可得CI=CD,再根据∠2+∠3=∠1+∠2=60°,可以证明∠1=∠3,然后即可证明△CDN与△CIN全等,从而得到重叠部分的面积等于以正六边形的边长为边的等边三角形的面积,即正六边形面积的$\frac{1}{6}$,进而解决问题.
解答 解:根据正六边形和正三角形的性质,可知CI=CD,
因为∠2+∠3=∠1+∠2=60°,所以∠1=∠3,
在△CIN和△CDM中,∠MDC=∠NIC=60°,CI=CD,∠1=∠3,
所以△CIM≌△CDM,
所以S△CIN=S△CDM,
所以重叠部分的面积是正六边形的$\frac{1}{6}$,即3×$\frac{1}{6}$=0.5(平方厘米)
所以阴影部分的面积为:
(2-0.5)+(3-0.5)
=1.5+2.5
=4(平方厘米)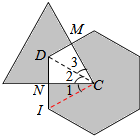
答:阴影部分的面积为4平方厘米.
点评 此题解答的关键在于求出正六边形的$\frac{1}{6}$的面积.进而得出空白部分的面积,解决问题.


科目:小学数学 来源: 题型:解答题
查看答案和解析>>
科目:小学数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com