
 如图,已知长方形ADEF的面积24,三角形ADB的面积是4,三角形ACF的面积是6,那么三角形ABC的面积是________.
如图,已知长方形ADEF的面积24,三角形ADB的面积是4,三角形ACF的面积是6,那么三角形ABC的面积是________.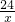 ;根据三角形ADB的面积是4,可求出BD的长度,进而求出BE的长度;根据三角形ACF的面积是6,可求出FC的长度,进而求出CE的长度;知道了BE和CE的长度,即可求出△BEC的面积,再用S矩形ADEF减去S△ADB减去S△ACF减去S△BCE,即得S△ABC.
;根据三角形ADB的面积是4,可求出BD的长度,进而求出BE的长度;根据三角形ACF的面积是6,可求出FC的长度,进而求出CE的长度;知道了BE和CE的长度,即可求出△BEC的面积,再用S矩形ADEF减去S△ADB减去S△ACF减去S△BCE,即得S△ABC.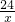 ;
; ×x×BD=4,
×x×BD=4, ,
,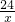 -
- =
=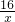 ;
; ×
×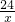 ×CF=6,
×CF=6, ,
, =
= ;
; ×
×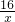 ×
× =4,
=4,

 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com