Question

10．如图．三角形ABC中．D是AB的中点．点E、F．G、H把BC平均分成五份．阴影部分的面积占三角形ABC面积的几分之几？

Answer 1

分析 要求阴影部分面积占三角形ABC面积的几分之几，就要推出阴影部分与三角形ABC面积之间的关系．如下图，连接DC、DE、DF，根据三角形底与面积的正比关系，先推出S阴影=$\frac{1}{5}$S△BDC；再根据△BDC与△ABC的面积关系，即可得出问题的答案．

解答 解：连结DC、DE、DF，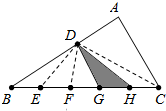

因为点E、F．G、H把BC平均分成五份，
所以S△DGH=$\frac{1}{5}$S△BDC；
因为D是AB的中点，
所以S△BDC=$\frac{1}{2}$S△ABC；
所以S△DGH=$\frac{1}{2}$×$\frac{1}{5}$S△ABC=$\frac{1}{10}$S△ABC
答：阴影部分的面积占三角形ABC面积的$\frac{1}{10}$．

点评 此题主要利用三角形的面积与底的正比关系，推出各三角形的面积关系，进而解决问题．