Question

求图中的每个小图形的阴影部分面积．

Answer 1

解：据分析解答如下：
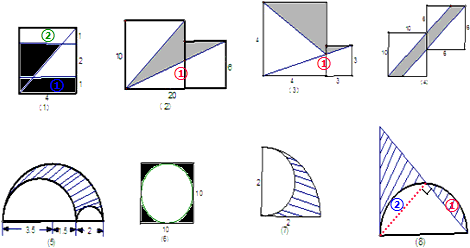
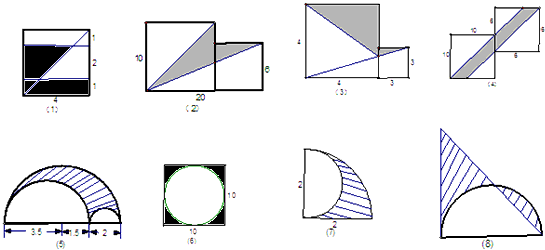
（1）4×4÷2=8（平方厘米）；
答：阴影部分的面积是8平方厘米．

（2）20×10÷2+6×6-（20+6）×6÷2，
=100+36-78，
=58（平方厘米）；
答：阴影部分的面积是58平方厘米．

（3）4×4÷2+3×3-（4+3）×3÷2，
=8+9-10.5，
=6.5（平方厘米）；
答：阴影部分的面积是6.5平方厘米．

（4）（6-4）×（10+4）=28（平方厘米）；
答：阴影部分的面积是28平方厘米．

（5）（3.5+1.5）÷2=2.5，2÷2=1，
[3.14×（3.5²-2.5²-1²）]÷2，
=[3.14×（12.25-6.25-1）]÷2，
=[3.14×5]÷2，
=15.7÷2，
=7.85（平方厘米）；
答：阴影部分的面积是7.85平方厘米．

（6）10×10-3.14×（10÷2）²，
=100-3.14×25，
=100-78.5，
=21.5（平方厘米）；
答：阴影部分的面积是21.5平方厘米．

（7）×3.14×2²-3.14×（2÷2）²÷2，
=3.14-1.57，
=1.57（平方厘米）；
答：阴影部分的面积是1.57平方厘米．

（8）8×8÷2=32（平方厘米）；
答：阴影部分的面积是32平方厘米．
分析：（1）将阴影梯形①旋转、平移到空白梯形②的位置，则阴影部分的面积等于正方形的面积的一半，利用正方形的面积公式即可求解；
（2）阴影部分的面积=长方形的面积的一半+小正方形的面积-下边的大三角形的面积（三角形①），利用长方形、正方形和三角形的面积公式即可求解；
（3）阴影部分的面积=小正方形的面积+大正方形的面积的一半-下边的大三角形的面积（三角形①），利用正方形和三角形的面积公式即可求解；
（4）阴影部分是一个平行四边形，其底和高分别为（6-4）厘米和（10+4）厘米，利用平行四边形的面积公式即可得解；
（5）阴影部分的面积=大半圆的面积-2个小空白半圆的面积，利用圆的面积公式即可求解；
（6）阴影部分的面积=正方形的面积-圆的面积，利用正方形和圆的面积公式即可求解；
（7）阴影部分的面积=圆的面积-空白半圆的面积，利用圆的面积公式即可求解；
（8）将阴影阴影①旋转、平移到空白②的位置，则阴影部分的面积等于三角形的面积的一半，利用三角形的面积公式即可求解．

点评：解答此题的关键是弄清楚：如何将阴影部分转换成规则图形，利用规则图形的面积和或差，即可求解．