Question

16．在一条直线上依次有A、B、C、D、E、F六个点，且相邻两个点之间的距离相等，下面能组成比例的是
 （　　）

• A． AC：BE=AD：CF
• B． AB：BD=CE：BC
• C． AB：CE=BD：AF
• D． BC：AC=AC：BF

Answer 1

分析 根据题意，可知AB=BC=CD=DE=EF，把每一段的距离看作1份数，那么两段就看作2份数，三段就看作3份数，四段就看作4份数，进而写出比例，再看两内项之积是否等于两外项之积，从而确定能否组成比例．

解答 解：见下图：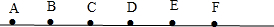

A、AC：BE=2：3，AD：CF=3：3，2：3和3：3，因为3×2≠3×3，所以不能组成比例；
B、AB：BD，1：2，CE：BC=3：1，1：2和3：1，因为1×1≠3×2，所以不能组成比例；
C、AB：CE，1：2，BD：AF=2：5，1：2和2：5，因为1×5≠2×2，所以不能组成比例；
D、BC：AC=1：2，AC：BF=2：4，1：2和2：4，因为1×4=2×2，所以能组成比例．
故选：D．

点评 解决此题关键是把相邻两个点之间的距离看作1份数，进而根据比例的性质解答．