Question

计算如图体积．（单位：分米）

（1）

 

；（2）

 

．

Answer 1

考点：组合图形的体积

专题：立体图形的认识与计算

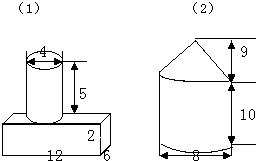
分析：（1）观察图（1）可知，这个几何体由一个圆柱和一个长方体组成，已知圆柱的底面直径为4分米，高为5分米；长方体的长12分米、宽6分米、高2分米，据此利用长方体的体积公式v=abh和圆柱体的体积公式v=sh代入数据计算即可；
（2）图（2）由一个圆柱体和一个底面积相等的圆锥体构成，底面直径都是8分米，圆柱高10分米，圆锥高9分米，利用圆柱的体积公式V=sh和圆锥的体积公式V=

1

3

sh列式解答即可．

解答： 解：（1）12×6×2+3.14×（4÷2）²×5
=144+3.14×4×5
=144+62.8
=206.8（立方分米）；
答：图（1）的体积是206.8立方分米．

（2）3.14×（8÷2）²×10+3.14×（8÷2）²×9×

1

3

=3.14×4²×10+3.14×4²×9×

1

3

=3.14×16×10+3.14×16×3
=502.4+150.72
=653.12（立方分米）；
答：图（2）的体积是653.12立方分米．
故答案为：（1）206.8立方分米；653.12立方分米．

点评：此题主要考查组合图形的体积，关键是明确组合图形是由哪些规则的立体图形组成，再利用立体图形的体积公式计算．