
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 99 |
| 1 |
| 99 |
| 3 |
| 10 |
| 5 |
| 1×2 |
| 5 |
| 2×3 |
| 5 |
| 3×4 |
| 5 |
| 99×100 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 99 |
| 1′ |
| 99 |
| 3 |
| 10 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 99 |
| 1 |
| 99 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 99 |
| 1′ |
| 99 |
| 1 |
| 2 |
| 3 |
| 2 |
| 2 |
| 3 |
| 4 |
| 3 |
| 3 |
| 4 |
| 5 |
| 4 |
| 98 |
| 99 |
| 100 |
| 99 |
| 1 |
| 2 |
| 100 |
| 99 |
| 50 |
| 100 |
| 3 |
| 10 |
| 5 |
| 1×2 |
| 5 |
| 2×3 |
| 5 |
| 3×4 |
| 5 |
| 99×100 |
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| 99×100 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 99 |
| 1 |
| 100 |
| 1 |
| 100 |
| 1 |
| 20 |
| 199 |
| 20 |


 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案科目:小学数学 来源: 题型:
| 口算题 7.2+2.8= |
0.7×16-16×0.2= | 6÷1.2= |
| 9.2÷2.3= | 24÷4+56÷4= | 1.5-4.5= |
| 30×(200+3)= | 12×2.5= | 2.5×0.4= |
| 0.36+0.64= | 4÷0.25= | 2.63+0.37= |
| 1.4×2.5×4= | 8.4÷4.2= | 4.8÷0.3= |
| 0.96÷0.3= | 8-2.5=8×1.5= | 2.73+1.5×4= |
查看答案和解析>>
科目:小学数学 来源: 题型:
| (1)200÷2÷5 | (2)9×(25+55) | (3)72÷8×6 | (4)6×19×5 |
| (5)949-260×3 | (6)2000-106×4 | (7)(31+77)×9 | (8)(206+103)÷3 |
| (9)80-75÷5 | (10)90+84÷4 | (11)15×2×5. |
查看答案和解析>>
科目:小学数学 来源: 题型:
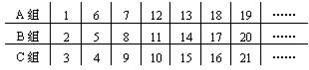 把自然数 1~200按下面的方法分成A、B、C三组.试问:
把自然数 1~200按下面的方法分成A、B、C三组.试问:查看答案和解析>>
科目:小学数学 来源: 题型:071
对策问题
在数学竞赛中,有一类很有趣味的智办游戏题,涉及到的课本知识并不多,但是技巧性比较强。在智力游戏中,对立者总是竭尽全力争取最大的胜利,不希望自己失败,因此对立者都认真选择对付对方的方法。用数学的观点和方法来研究取胜的策略叫做对策问题。
提问 有
200枚围棋子放在盒子里,甲、乙两个轮流各取1枚或2枚,取到最后一枚为胜者,必胜的对策是什么?解 由于每人可取
1枚或2枚,当甲取1枚时,乙可以取2枚,当甲取2枚时,乙可以取1枚,所以不妨将3枚棋子作为一组。由200÷3=66(组)……2(枚),为了确保拿到这堆棋子的最后一枚或2枚,甲应争取先拿,且拿走2枚,然后乙随便取1枚或2枚,甲就相应地取2枚或1枚,以使得两人各取一次后一共取走3枚,这样甲就必是胜方。查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com