
分析 (1)首先根据比例的基本性质化简,然后根据等式的性质,两边同时除以$\frac{2}{5}$即可.
(2)首先根据比例的基本性质化简,然后根据等式的性质,两边同时除以4即可.
(3)首先根据等式的性质,两边同时减去8.5,然后两边再同时除以0.65即可.
解答 解:(1)$\frac{4}{5}$:$\frac{2}{5}$=x:36
$\frac{2}{5}$x=36×$\frac{4}{5}$
$\frac{2}{5}$x=$\frac{144}{5}$
$\frac{2}{5}$x$÷\frac{2}{5}$=$\frac{144}{5}$$÷\frac{2}{5}$
x=72
(2)$\frac{x}{1.2}$=$\frac{0.5}{4}$
4x=1.2×0.5
4x=0.6
4x÷4=0.6÷4
x=0.15
(3)8.5+65%x=15
8.5+0.65x-8.5=15-8.5
0.65x=6.5
0.65x÷0.65=6.5÷0.65
x=10
点评 此题主要考查了根据等式的性质解方程的能力,即等式两边同时加上或同时减去、同时乘以或同时除以一个数(0除外),两边仍相等.


科目:小学数学 来源: 题型:计算题
查看答案和解析>>
科目:小学数学 来源: 题型:解答题
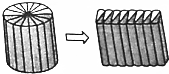 一个圆柱的侧面积与底面积的比是4:1,把这个圆柱沿底面半径分成若干等份,拼成了一个与圆柱等底等高的近似长方体(如图所示),这个近似长方体的底面周长是16.56厘米,原来圆柱的体积是多少立方厘米?
一个圆柱的侧面积与底面积的比是4:1,把这个圆柱沿底面半径分成若干等份,拼成了一个与圆柱等底等高的近似长方体(如图所示),这个近似长方体的底面周长是16.56厘米,原来圆柱的体积是多少立方厘米?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com