
分析 把这项工程的工作量看作单位“1”,甲、乙两人合作需要8天完成,甲、乙每天的工作效率和是$\frac{1}{8}$,乙独做,需12天完成,那么乙平均每天的工作效率为$\frac{1}{12}$,由此可以求出甲平均每天的工作效率为$\frac{1}{8}-\frac{1}{12}$=$\frac{1}{24}$,根据工作效率×工作时间=工作量,求出甲3天完成了总工作量的几分之几,然后用剩下的工作量除以甲、乙的工作效率和即可.据此解答.
解答 解:甲平均每天的工作效率:$\frac{1}{8}-\frac{1}{12}$=$\frac{1}{24}$,
(1$-\frac{1}{24}×$3)$÷\frac{1}{8}$
=(1$-\frac{1}{8}$)$÷\frac{1}{8}$
=$\frac{7}{8}÷\frac{1}{8}$
=$\frac{7}{8}×8$
=7(天),
答:两人合作了7天.
点评 此题主要考查工作时间、工作效率、工作总量三者之间的数量关系,解答时往往把工作总量看作“1”,再利用它们的数量关系解答.


科目:小学数学 来源: 题型:解答题
查看答案和解析>>
科目:小学数学 来源: 题型:解答题
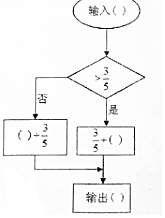 按照流程图回答下列问题,写出必要的计算过程.
按照流程图回答下列问题,写出必要的计算过程.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com