


科目:小学数学 来源: 题型:071
1.画示意图
图形具有直观性,但在实际数学问题中的具体含义、具体条件以及数量关系往往比较隐蔽,比较复杂,那么画示意图是指将实际数学问题中隐藏复杂的内涵条件以及复杂的数量关系画出示意图,用几何图形直观形象地表示出来,这样不仅简单明了,而且容易从整体上把握题目,便于思考和求解,俗话说:“一图顶千言。”
2.在计数问题中常见的几种示意图
(1)画线段图。即把文字的含义用线段表示出来,例如“组队问题”“和差问题”和倍问题”“行程问题”等等,用线段图解起来往往比文字的叙述更简单明了得多。
如:用
1、2、3、4四个数中两个数组成一个两位数,试求有几种不同的组合方法?①用
A、B、C、D四点分别表示1、2、3、4,画出线段图:
②线段的条数与组合方案数之间的关系是
________。(2)画“树图”。什么样的图叫做“树图”呢?请看实例:
从甲村到乙村有两条路可走,从乙村到丙村有三条路可走
(如图(a)),那么从甲村到丙村有几条路可走呢?
根据题意可知,从甲村到乙村的每条道路都对应着从乙村到丙村的三条道路,于是我们可画出如图
b的图形,这图形中明显地告诉我们,从甲村到丙村有________条路可走。在数学上将类似上图的这种没有回路的图形叫做“树图”,现实生活中最典型的“树图”是家谱。在数学学习中,画“树图”是计数问题中最基本的思考方法。
3.需要同学们注意的是,数学问题来自于生活实际,千变万化、错综复杂、灵活性很强,在计数时,实际应用绝不能拘泥于这几种示意图。比如连线图、阶梯图等等,要因题而定,只要画出的示意图能帮助思考,推理或简化解答都可以。
查看答案和解析>>
科目:小学数学 来源:数学教研室 题型:072
1.画示意图
图形具有直观性,但在实际数学问题中的具体含义、具体条件以及数量关系往往比较隐蔽,比较复杂,那么画示意图是指将实际数学问题中隐藏复杂的内涵条件以及复杂的数量关系画出示意图,用几何图形直观形象地表示出来,这样不仅简单明了,而且容易从整体上把握题目,便于思考和求解,俗话说:“一图顶千言。”
2.在计数问题中常见的几种示意图
(1)画线段图。即把文字的含义用线段表示出来,例如“组队问题”“和差问题”和倍问题”“行程问题”等等,用线段图解起来往往比文字的叙述更简单明了得多。
如:用
1、2、3、4四个数中两个数组成一个两位数,试求有几种不同的组合方法?①用
A、B、C、D四点分别表示1、2、3、4,画出线段图:
②线段的条数与组合方案数之间的关系是
________。(2)画“树图”。什么样的图叫做“树图”呢?请看实例:
从甲村到乙村有两条路可走,从乙村到丙村有三条路可走
(如图(a)),那么从甲村到丙村有几条路可走呢?
根据题意可知,从甲村到乙村的每条道路都对应着从乙村到丙村的三条道路,于是我们可画出如图
b的图形,这图形中明显地告诉我们,从甲村到丙村有________条路可走。在数学上将类似上图的这种没有回路的图形叫做“树图”,现实生活中最典型的“树图”是家谱。在数学学习中,画“树图”是计数问题中最基本的思考方法。
3.需要同学们注意的是,数学问题来自于生活实际,千变万化、错综复杂、灵活性很强,在计数时,实际应用绝不能拘泥于这几种示意图。比如连线图、阶梯图等等,要因题而定,只要画出的示意图能帮助思考,推理或简化解答都可以。
查看答案和解析>>
科目:小学数学 来源:数学教研室 题型:072
议一议
(1)
正六边形能否密铺?简述你的理由。(2)
分析图,讨论正五边形不能密铺的原因。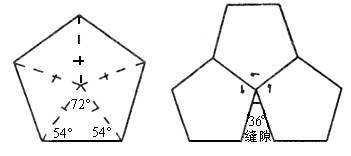
(3)
还能找到能密铺的其他正多边形吗?通过上述问题的探讨研究,可以看出对于给定的某种正多边形,它能否拼成一个平面图形,既不留下一丝空白,又不相互重叠,显然与它的内角大小有关。为了探索哪些正多边形能铺满平面,请根据图,用计算器或量角器完成下表:

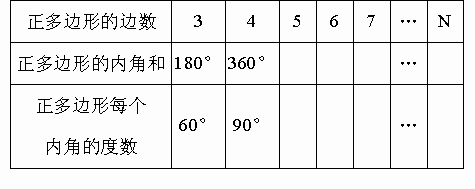
通过上面研讨和计算,我们可以发现:当围绕一点拼在一起的几个多边形的内角加在一起恰好组成一个周角时,就拼成一个平面图形。
如正六边形的每个内角为
120°,三个120°拼在一起恰好组成周角,所以全用正六边形瓷砖就可以铺满地面。所以用相同的正多边形拼地板或用两种以上的正多边形拼地板都可以达到密铺的目的,甚至一些不规则的图形也可以做到,如图所示。
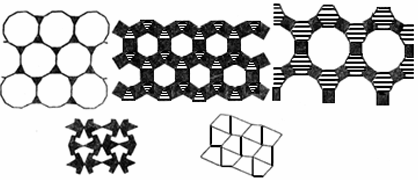
通过这节的学习,你学到了哪些知识,有哪些收获,能否运用你所学过的知识试着完成下列问题。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com