
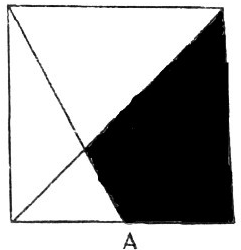
分析 如图,A为所在边的中点,求出AB的长,运用三角形面积公式求出三角形ABE的面积,再求出三角形DEF的面积,然后用正方形面积减去这两个三角形的面积即可.
解答 解:如图,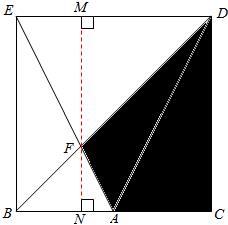
如图:因为A为所在边的中点,所以AB=12÷2=6(厘米),
△ABE的面积:6×12÷2
=72÷2
=36(平方厘米)
12:6=2:1,所以△EFD是△ABF按2:1放大并旋转后的图形,
因此这两个三角形的高MF:NF的比是2:1,
12÷(2+1)×2
=12×2
=8(厘米)
12×8÷2
=96÷2
=48(平方厘米)
12×12-36-48
=144-36-48
=60(平方厘米)
答:阴影部分面积为60平方厘米.
点评 本题属于求组合图形面积的问题,这种类型的题目主要明确组合图形是由哪些基本的图形构成的,然后看是求几种图形的面积和还是求面积差,然后根据面积公式解答即可.


 阅读快车系列答案
阅读快车系列答案科目:小学数学 来源: 题型:解答题
查看答案和解析>>
科目:小学数学 来源: 题型:解答题
| 班级 | 班级总人数 | 三好学生人数 | 三好学生人数占班级总人数的百分之几 |
| 五(1)班 | 40 | 9 | |
| 五(2)班 | 9 | 18% | |
| 五(3)班 | 20% | ||
| 合计 | 135 | 27 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com