
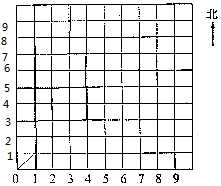
 如图,如果一个小正方形的对角线长20cm,则点(2,2)东偏北45°方向60cm处是点(5,5);点(5,2)南偏西45°方向40cm处是点(3,0);点(7,6)北偏西45°方向20cm处是点(6,7)
如图,如果一个小正方形的对角线长20cm,则点(2,2)东偏北45°方向60cm处是点(5,5);点(5,2)南偏西45°方向40cm处是点(3,0);点(7,6)北偏西45°方向20cm处是点(6,7) 分析 根据用数对表示点的位置的方法,第一个数字表示列数,第二个数字表示行数,即可在图中描出(2,2)所表示的点的位置A;根据平面图上的方向,上北下南,左西右东,以A为观测点即可确定东偏北45°方向60cm处点A′的位置,并用数对表示出来;同理可画出点B(5,2)南偏西45°方向40cm处点B′的位置;点C(7,6)北偏西45°方向20cm处点C′的位置.
解答 解:如图: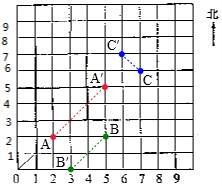
如果一个小正方形的对角线长20cm,则点(2,2)东偏北45°方向60cm处是点(5,5);点(5,2)南偏西45°方向40cm处是点(3,0);点(7,6)北偏西45°方向20cm处是点(6,7).
故答案为:5,5;3,0;6,7.
点评 此题考查的知识有数对与位置、根据方向和距离确定物体的位置.无特殊说明的情况下,数对中第一个数字表示列,第二个数字表示行;根据方向的距离确定物体的位置关键是观测点的确定.


科目:小学数学 来源: 题型:选择题
| A. | (3.2×1.5+2.5)÷1.6 | B. | 3.2×(1.5+2.5)÷1.6 | C. | 3.2×1.5+2.5÷1.6 | D. | 1.6÷[3.2÷(1.5+2.5)] |
查看答案和解析>>
科目:小学数学 来源: 题型:解答题
查看答案和解析>>
科目:小学数学 来源: 题型:填空题
查看答案和解析>>
科目:小学数学 来源: 题型:计算题
| 1+$\frac{1}{7}$= | $\frac{5}{8}$-$\frac{1}{8}$= | 1-$\frac{1}{7}$-$\frac{3}{7}$= | $\frac{1}{4}$+$\frac{1}{5}$+$\frac{4}{5}$= | 1-0.98= |
| $\frac{1}{3}$+$\frac{5}{12}$= | $\frac{1}{2}$+1$\frac{1}{3}$= | $\frac{5}{12}$+$\frac{7}{12}$= | $\frac{7}{16}$-$\frac{5}{16}$+$\frac{7}{8}$= | 5×0.05= |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com