Question

【题目】（1）请你在边长是3厘米的正方形中画一个最大的圆．

（2）如果该正方形的面积是25平方厘米，写出正方形的面积与正方形里最大圆面积的比．

Answer 1

【答案】（1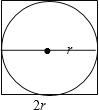）（2）200：157．

【解析】

试题分析：（1）正方形内最大的圆的直径等于正方形的边长，由此以正方形的中心为圆心，以边长为直径画圆；

（2）设圆的半径为r，则正方形的边长就是2r，即2r×2r=4r2=25，所以得出r2=，代入圆的面积公式中即可求得这个最大圆的面积，从而解决问题．

解：（1）以正方形的中心为圆心，以边长为直径画圆，如图所示；

（2）设圆的半径为r，则正方形的边长就是2r，所以：

2r×2r=4r2=25，所以得出r2=，

则圆的面积是：3.14×=，

所以正方形的面积与圆的面积之比：25：=200：157，

答：正方形与最大圆的面积之比是200：157．