用同一根绳子分别围成一个正方形和一个圆,圆的面积一定比正方形的面积大.________.
正确
分析:要比较周长相等的正方形和圆形,谁的面积最大,谁面积最小,可以先假设这两种图形的周长是多少,再利用这两种图形的面积公式,分别计算出它们的面积,最后比较即可.
解答:为了便于理解,假设正方形、长方形和圆形的周长都是16,
则圆的半径为:
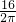
=
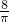
,
面积为:π×
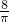
×
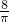
=
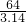
=20.38;
正方形的边长为:16÷4=4,面积为:4×4=16;
所以周长相等的正方形和圆形,圆面积最大.原题说法正确.
故答案为:正确.
点评:此题主要考查正方形、圆形的面积公式及灵活运用,解答此题可以先假设这两种图形的周长是多少,再利用这两种图形的面积公式,分别计算出它们的面积,最后比较这两种图形面积的大小.

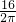 =
=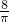 ,
,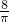 ×
×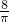 =
=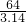 =20.38;
=20.38;
