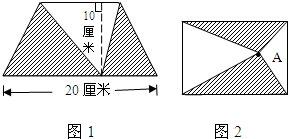
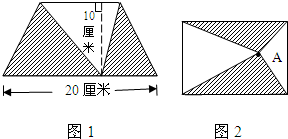
分析:(1)因为BC=12厘米,所以BE=
×12=4厘米,则EC=12-4=8厘米,
所以当时间t=0时,如图,三角形AEP的面积是:8×20÷2=80平方厘米;
当t=1、2、3、4秒时△AEP的面积=长方形ABCD的面积-三角形ABE的面积-三角形ACP的面积-三角形DEP的面积,
当t=5秒时,点P与点D重合,如图3,三角形APE的面积直接利用三角形的面积公式即可解答,由此根据路程=速度×时间,先求出PC的长度即可解决问题;
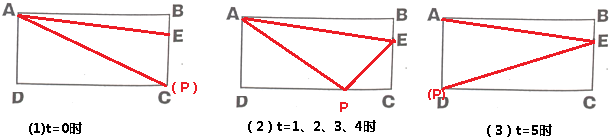
(2)(t=5时三角形的面积减去t=0时三角形APE的面积)÷5就是这个三角形面积增长的平均速度.
解答:解:(1)长方形ABCD的面积是:20×12=240(平方厘米),
因为BC=12厘米,所以BE=
×12=4(厘米),
则EC=12-4=8(厘米),三角形ABE的面积=4×20÷2=40(平方厘米);
所以当时间t=0时,三角形AEP(即三角形AEC)的面积是:8×20÷2=80平方厘米;
当t=1时,PC=4×1=4(厘米),则三角形AEP的面积是:
240-(20-4)×12÷2-4×8÷2-40,
=240-96-16-40,
=88(平方厘米),
当t=2时,PC=4×2=8(厘米),则三角形AEP的面积是:
240-(20-8)×12÷2-8×8÷2-40,
=240-72-32-40,
=96(平方厘米),
当t=3时,PC=4×3=12(厘米),则三角形AEP的面积是:
240-(20-12)×12÷2-12×8÷2-40,
=240-48-48-40,
=104(平方厘米),
当t=4时,PC=4×4=16(厘米),则三角形AEP的面积是:
240-(20-16)×12÷2-16×8÷2-40,
=240-24-64-40,
=112(平方厘米),
当t=5时,PC=5×4=20,此时P与D重合,则三角形AEP的面积是:
12×20÷2=120(平方厘米),
答:当时间t=0、1、2、3、4、5秒时△AEP的面积分别是:80平方厘米、88平方厘米、96平方厘米、104平方厘米、112平方厘米、120平方厘米.
(2)这些三角形的面积平均增长速度是:(120-80)÷5,
=40÷5,
=8(平方厘米),
答:平均每秒增长8平方厘米.

 如图,是一个长方形ABCD,AB=20cm,BC=12cm,BC的三分之一处有一固定的点E,在C处有一个能移动的点P.点P以每秒4cm的速度向D点移动,求:
如图,是一个长方形ABCD,AB=20cm,BC=12cm,BC的三分之一处有一固定的点E,在C处有一个能移动的点P.点P以每秒4cm的速度向D点移动,求:


 如图,有一个长方形棋盘,每个小方格的边长都是1厘米,长有200格,宽有150格,纵横线交叉的点称为格点.那么,连结A、B两点的线段一共经过
如图,有一个长方形棋盘,每个小方格的边长都是1厘米,长有200格,宽有150格,纵横线交叉的点称为格点.那么,连结A、B两点的线段一共经过