
分析 根据给出的新运算f(x)=$\frac{x+3}{3x+1}$,由此用此方法求出f($\frac{1}{2}$)的值,然后再表示出f($\frac{1}{2}$)的小数部分与不超过f($\frac{1}{2}$)的最大整数即可.
解答 解:f($\frac{1}{2}$)
=$\frac{\frac{1}{2}+3}{3×\frac{1}{2}+1}$
=$\frac{3.5}{2.5}$
=3.5÷2.5
=1.4;
(1.4)=0.4,【1.4】=1;
所以,(f($\frac{1}{2}$))=0.4,【f($\frac{1}{2}$)】=1.
点评 本题关键是根据给出的新的运算方法,求出f($\frac{1}{2}$),然后再进一步解答.


科目:小学数学 来源: 题型:解答题
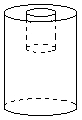 有一个圆柱体的零件,高10厘米,底面直径是6厘米,零件的一端有一个圆柱形的圆孔,圆孔的直径是4厘米,孔深5厘米(见图).如果将这个零件接触空气的部分涂上防锈漆,那么一共要涂多少平方厘米?
有一个圆柱体的零件,高10厘米,底面直径是6厘米,零件的一端有一个圆柱形的圆孔,圆孔的直径是4厘米,孔深5厘米(见图).如果将这个零件接触空气的部分涂上防锈漆,那么一共要涂多少平方厘米?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com