
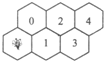
 一只蜜蜂在左下角,由于受了伤,只能爬行,不能飞,始终向右方(右上、右下)爬行,如图,从一间蜂房爬到右边相邻的蜂房中.问:蜜蜂从最初位置爬到4号蜂房共有多少种不同的爬法?
一只蜜蜂在左下角,由于受了伤,只能爬行,不能飞,始终向右方(右上、右下)爬行,如图,从一间蜂房爬到右边相邻的蜂房中.问:蜜蜂从最初位置爬到4号蜂房共有多少种不同的爬法?

科目:小学数学 来源: 题型:
查看答案和解析>>
科目:小学数学 来源: 题型:
 有一排蜂房,形状如图,一只蜜蜂在左下角,假定蜜蜂只能爬行,不能飞,而且始终向右方(包括右上,右下)爬行,从一间蜂房爬到右边相邻的蜂房中去.例如.蜜蜂爬到1号蜂房的爬法有:蜜蜂→1号;蜜蜂→0号→1号,共有2种不同的爬法.问蜜蜂从最初位置爬到4号蜂房共有( )种不同的爬法.
有一排蜂房,形状如图,一只蜜蜂在左下角,假定蜜蜂只能爬行,不能飞,而且始终向右方(包括右上,右下)爬行,从一间蜂房爬到右边相邻的蜂房中去.例如.蜜蜂爬到1号蜂房的爬法有:蜜蜂→1号;蜜蜂→0号→1号,共有2种不同的爬法.问蜜蜂从最初位置爬到4号蜂房共有( )种不同的爬法.查看答案和解析>>
科目:小学数学 来源:一课一练 题型:042
有两个自行车运动员同时在公路上训练,行车方向是相向的.有一只蜜蜂对他们的练习很关心,当他们还相距300千米时,它从一个运动员的肩上开始向另一个运动员飞去,它碰上那个运动员后,又马上飞回来.就这样在两个运动员之间飞来飞去,直到他们相遇.蜜蜂是以每小时100千米的速度在两个运动员之间飞的,在这段时间里两个运动员行驶的速度都是每小时50千米.那么,蜜蜂一共飞行了多少千米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com