
【题目】如图是一个由9个相同的小等边三角形所组成的大等边三角形,现在要把一枚黑子和一枚白子分别放入两个小等边三角形中,并且要求这两个小等边三角形既没有公共边也没有公共顶点,那么共有( )种不同的放置方法。
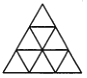
A. 22 B. 24 C. 25 D. 28
【答案】B
【解析】 本题考查学生枚举的功底及对三角形中对称性的认识。图形的特殊性决定了本题很难直接用乘法原理解决。
枚举黑子的放置情况,当把黑子依次放在每个小等边三角形中时,我们把放置相应的白子的方法数写在小等边三角形内(如图1),例如“5”表示把黑子放在这一格时,相应的白子有5种放法(如图2)
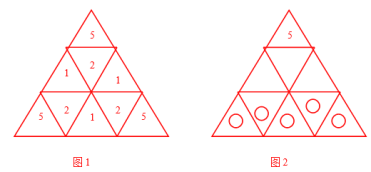
例如“2”表示把黑子放在这一格时,相应的白子有2种放法(如图3)
例如“1”表示把黑子放在这一格时,相应的白子有1种放法(如图4)
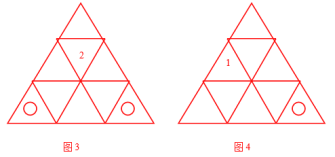
一共有(5+2+1) ×3=24种不同的放置方法。


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:小学数学 来源: 题型:
【题目】125×6+125×4的简便算法是( )
A. 125×(6+4)B. 125×6×4C. (125×6)×(125×4)D. (125×125)×(6+4)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com