
分析 也就是第一根绳子长的$\frac{1}{2}$等于第二根绳子长的(1-$\frac{1}{3}$),即$\frac{2}{3}$,很显然第一根据绳子长一些.
解答 解:用两根绳子测井深,第一根绳子露在井口外$\frac{1}{2}$,第二根绳子露在井口外$\frac{1}{3}$,
第一根绳子长度×$\frac{1}{2}$=第二根绳长度×(1-$\frac{1}{3}$),
则,第一根绳子长度=第二根绳长度×(1-$\frac{1}{3}$)×2=第二根绳长度×$\frac{4}{3}$,
如果两根绳子在井口里的长度相等,那么第一根绳子长一些.
故答案为:一.
点评 井内绳子长度相等,井外哪个根剩的多哪根长一些.


科目:小学数学 来源: 题型:解答题
查看答案和解析>>
科目:小学数学 来源: 题型:填空题
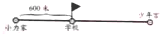 如图,小力家与学校、少年宫在一条直路上,小力从家步行到学校用了12分,已走了从家到少年宫总路程的$\frac{2}{5}$,照这样的速度,小力继续从学校步行到少年宫还要18分.
如图,小力家与学校、少年宫在一条直路上,小力从家步行到学校用了12分,已走了从家到少年宫总路程的$\frac{2}{5}$,照这样的速度,小力继续从学校步行到少年宫还要18分.查看答案和解析>>
科目:小学数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com