
分析 将一个等边三角形的三条边分别延长$\frac{1}{3}$,则新三角形的边长是原三角形边长的1+$\frac{1}{3}$=$\frac{4}{3}$,因为扩大前后两个等边三角形相似,根据相似三角形的性质:面积的比等于相似比的平方求解即可.
解答 解:将一个等边三角形的三条边分别延长$\frac{1}{3}$,则新三角形的边长是原三角形边长的1+$\frac{1}{3}$=$\frac{4}{3}$,
两三角形的相似比为$\frac{4}{3}$:1
根据相似三角形的性质:面积为原来的$\frac{16}{9}$倍,
所以面积扩大了$\frac{16}{9}$-1=$\frac{7}{9}$,
答:得到的新三角形的面积比原来增加了$\frac{7}{9}$.
点评 本题考查对相似三角形性质的理解.(1)相似三角形周长的比等于相似比;(2)相似三角形面积的比等于相似比的平方;(3)相似三角形对应高的比、对应中线的比、对应角平分线的比都等于相似比.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:小学数学 来源: 题型:填空题
| 保留整数 | 保留一位小数 | 保留两位小数 | |
| 8.935 | 9 | 8.9 | 8.94 |
| 0.906 | 1 | 0.9 | 0.91 |
| 55.463 | 55 | 55.5 | 55.46 |
查看答案和解析>>
科目:小学数学 来源: 题型:操作题
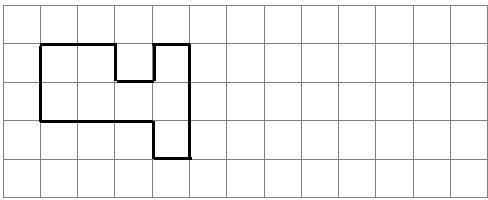
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com