Question

【题目】已知函数,函数.

(1)当时,求函数的表达式；

(2)若，函数在上的最小值是，求的值；

(3)在(2)的条件下,求直线与函数的图象所围成图形的面积.

Answer 1

【答案】（1）；（2）；（3）.

【解析】试题分析：(1)讨论两种情况，求出结果相同，直接代入，即可得函数的表达式；(2)利用基本不等式求得函数在上的最小值是由，可得的值；（3）先求得直线与函数的图象的交点坐标，直线与函数的图象所围成图形的面积就是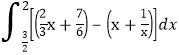,从而可得结果.

试题解析：

(1)因为f(x)=ln|x|,所以当x>0时,f(x)=lnx,f′(x)=,

当x<0时,f(x)=ln(-x),f′(x)=·(-1)=.所以当x≠0时,函数y=g(x)=x+.

(2)因为由(1)知当x>0时,g(x)=x+,

所以当a>0,x>0时,g(x)≥2,当且仅当x=时取等号.所以函数y=g(x)在(0,+∞)上的最小值是2,所以依题意得2=2,所以a=1.

(3)由解得所以直线y=x+与函数y=g(x)的图象所围成图形的面积S=dx=+ln3-2ln2.