
 如图是一个正方形,边长6厘米,E、F分别是CD、BC的中点,求阴影部分的面积.
如图是一个正方形,边长6厘米,E、F分别是CD、BC的中点,求阴影部分的面积. =
= =
= =0.5,
=0.5,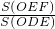 =0.5,
=0.5, S(DEF)=1.5(平方厘米),
S(DEF)=1.5(平方厘米), =
= =
= =0.5,因为等高三角形面积比等于底边比,所以
=0.5,因为等高三角形面积比等于底边比,所以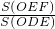 =0.5,又因为S(OEF)+S(ODE)=S(DEF)=0.5S(CDF)=S(CEF)=4.5(平方厘米),所以S(EOF)=
=0.5,又因为S(OEF)+S(ODE)=S(DEF)=0.5S(CDF)=S(CEF)=4.5(平方厘米),所以S(EOF)= S(DEF)=1.5(平方厘米),S空白=S(DEF)+S(BCE)-S(EOF)-S(CEF)=9+9-1.5-4.5=12(平方厘米),所以S阴影=S(ABCD)-S空白=36-12=24(平方厘米)
S(DEF)=1.5(平方厘米),S空白=S(DEF)+S(BCE)-S(EOF)-S(CEF)=9+9-1.5-4.5=12(平方厘米),所以S阴影=S(ABCD)-S空白=36-12=24(平方厘米)

 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com