
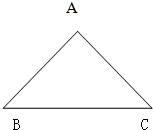
 (1)以BC为底边,过三角形的A点画一条与BC平行的直线,并画出底边上的高.再量出底边是4.5厘米,高是2.5厘米.
(1)以BC为底边,过三角形的A点画一条与BC平行的直线,并画出底边上的高.再量出底边是4.5厘米,高是2.5厘米.分析 (1)把三角板的一边与BC重合,另边紧靠一直尺,沿直尺滑动三角板,当原来与BC重合的一边经过点A时,沿这边画直线MN,则MN∥BC;然后再用刻度尺量出三角形ABC的底BC是多少厘米;再把三角板一条直角边与BC重合,沿BC边滑动三角板,当另一直角边经过点A时,没这边画线段AD,则AD就是三角形ABC的高,并能刻度尺量出是多少厘米.
(2)在直线MN上取一点E,使∠EBC为钝角,连结CE,则三角形BCE就是与三角形ABC等面积的钝角三角形.
(3)这个钝角三角形的底、高分别与三角形ABC的底、高相等,根据三角形面积计算公式“S=$\frac{1}{2}$ah”即可求出它的面积.
解答 解:(1)以BC为底边,过三角形的A点画一条与BC平行的直线,并画出底边上的高(下图):
再量出底边BC=4.5厘米,高是AD=2.5厘米.
(2)画出一个钝角三角形,使钝角三角形与三角形ABC的面积相等(图中三角形BCE).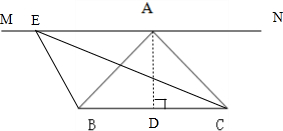
(3)4.5×2.5×$\frac{1}{2}$
=11.25×$\frac{1}{2}$
=5.625(平方厘米)
答:求这个钝角三角形的面积5.625平方厘米.
故答案为:4.5,2.5.
点评 此题主要考查三角形的高的意义以及高的画法,和过已知直线外的一点画已知直线的平行线的方法,明确等底等高的三角形的面积相等.


 智能训练练测考系列答案
智能训练练测考系列答案科目:小学数学 来源: 题型:计算题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com