Question

10．一个长方体水箱，长50cm，宽40cm，高70cm，水箱上部安装了一个进水管A，底部安装了一个放水管B．先开A管，过一段时间后接着打开B管，如图表示水箱中水位的变化情况，求：水位/cm

①几分后两管同时打开，这时水深多少cm？
②A管每分进水多少cm³，B管每分放水多少cm^3？
③A、B两管的内径相同，A管的进水速度为3米/秒，则B管的放水速度为多少米/秒？

Answer 1

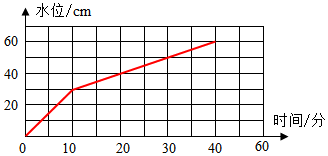
分析 ①观察统计图知道，10分钟后两管同时打开，这时水深是30厘米；
②前10分钟进水的水位深是30厘米，明显B管没有开，由此算出A管每分钟的进水的水位高度；A和B同时开放（20-10）分钟内进水的水位高度的变化是（40-30）厘米，由此得出B管每分钟放水的水位高度是1厘米，再根据长方体的体积公式，即可求出A管每分钟进水的体积与B管每分钟放水的体积；
③A和B同时开放，（20-10）分钟内进水的水位高度的变化是（40-30）厘米，所以每分钟进水的高度是（40-30）÷（20-10）厘米，此时A管的进水速度是3米/秒，所以B水管的放水速度即可求出．

解答 解：①从统计图知道，10分钟后两管同时打开，这时水深是40cm；

②50×40×（30÷10）
=2000×3
=6000（cm³）；
50×40×[（30÷10）-（40-30）÷（20-10）]
=2000×[3-1]
=4000（cm³）
答：A管每分进水6000cm³，B管每分放水4000cm³．

③3-1=2（米/秒），
答：B管的放水速度为2米/秒．
故答案为：10，30；6000，4000；2．

点评 本题考查了统计图表的综合应用．解答此题的关键是，能够看懂统计图，并能根据要求的问题从中获取有用的信息．