
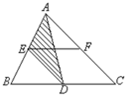
 已知三角形ABC的面积为56平方厘米、是平行四边形DEFC的2倍,那么阴影部分的面积是
已知三角形ABC的面积为56平方厘米、是平行四边形DEFC的2倍,那么阴影部分的面积是

 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:小学数学 来源:优等生数学 六年级 题型:041
如图,已知三角形ABC的面积为2平方厘米,延长AB至D,使AD=3AB;延长BC至E,使BE=4BC;延长CA至F,使CF=2CA.求三角形DEF的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com