
分析 (1)通过观察,此题把每个数凑成整数,然后再进行简算.
(2)把带分数化为假分数,约分后变为999×998+997,然后把999看作1000-1,进一步计算即可.
(3)此题数字非常接近,可通过数字拆分进行简算,把1997.05看作1999.05-2,运用乘法分配律简算.
(4)通过观察,可把6666看作3×2222,原式变为9999×7777+9999×2222,运用乘法分配律简算.
(5)原式变为2004×1000100010001÷(4002×1000100010001),从而进行简算.
解答 解:(1)89+899+8999+89999+899999
=(90-1)+(900-1)+(9000-1)+(90000-1)+(900000-1)
=999990-5
=999985
(2)999$\frac{997}{998}$÷$\frac{1}{499}$
=$\frac{999×998+997}{998}$×499
=(999×998+997)÷2
=[(1000-1)×998+997]÷2
=[998000-998+997]÷2
=[998000-1]÷2
=997999÷2
=498999.5
(3)2004.05×1997.05-2001.05×1999.05
=2004.05×(1999.05-2)-2001.05×1999.05
=2004.05×1999.05-2004.05×2-2001.05×1999.05
=(2004-2001)×1999.05-2004.05×2
=3×1999.05-2×2004.05
=3×1999+3×0.05-2×2000-2×4.05
=3×2000-3+0.15-2×2000-8.10
=2000-3+0.15-8.10
=2000+0.15-11.10
=1989.05
(4)9999×7777+3333×6666
=9999×7777+3333×3×2222
=9999×7777+9999×2222
=9999×(7777+2222)
=9999×9999
=(10000-1)×9999
=99990000-9999
=999890001
(5)2004200420042004÷4002400240024002
=2004×1000100010001÷(4002×1000100010001)
=2004÷4002
=$\frac{1002}{2001}$
点评 此题主要考查学生能否根据数字特点,通过转化的数学思想,巧妙灵活地运用运算定律,使复杂的问题简单化.


科目:小学数学 来源: 题型:操作题
 (1)经过红星村向东偏北30度筑一条318国道,请用线画出这条国道的位置.
(1)经过红星村向东偏北30度筑一条318国道,请用线画出这条国道的位置.查看答案和解析>>
科目:小学数学 来源: 题型:解答题
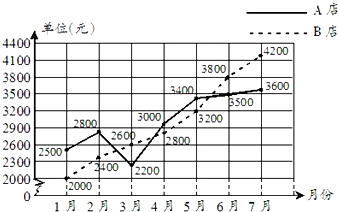 如图是张叔叔家开的A、B两家水果店去年1~7月营业额统计图.
如图是张叔叔家开的A、B两家水果店去年1~7月营业额统计图.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com