
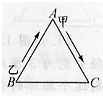
 如图所示是一个边长为120m的等边三角形,甲乙同时分别从A点,B点按顺时针方向出发,甲每分钟走120m,乙每分钟走180m,但经过每个顶点时,因转弯都要耽误5s,则乙出发
如图所示是一个边长为120m的等边三角形,甲乙同时分别从A点,B点按顺时针方向出发,甲每分钟走120m,乙每分钟走180m,但经过每个顶点时,因转弯都要耽误5s,则乙出发

 培优三好生系列答案
培优三好生系列答案科目:小学数学 来源: 题型:
 (1)量一量,如图所示正方形的边长是
(1)量一量,如图所示正方形的边长是查看答案和解析>>
科目:小学数学 来源: 题型:
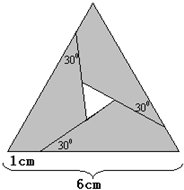 如图所示,把边长为6cm的等边三角形剪成4部分,从三角形顶点往下1cm处,呈30°角下剪刀,使中间部分形成一个小的等边三角形.
如图所示,把边长为6cm的等边三角形剪成4部分,从三角形顶点往下1cm处,呈30°角下剪刀,使中间部分形成一个小的等边三角形.查看答案和解析>>
科目:小学数学 来源: 题型:
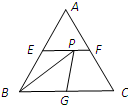 如图所示,在边长为2的正三角形ABC中,E、F、G分别为AB、AC、BC的中点,点P线段EF上一个动点,连接BP、GP,则△BPG周长的最小值是
如图所示,在边长为2的正三角形ABC中,E、F、G分别为AB、AC、BC的中点,点P线段EF上一个动点,连接BP、GP,则△BPG周长的最小值是查看答案和解析>>
科目:小学数学 来源: 题型:解答题
 (1)量一量,如图所示正方形的边长是______厘米.
(1)量一量,如图所示正方形的边长是______厘米.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com