Question

10．图中阴影部分是扇形的一部分，扇形的半径是6厘米，求阴影的面积．

Answer 1

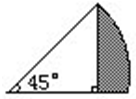
分析 观察图形可知，图中的空白三角形是一个斜边长为6厘米的等腰直角三角形，设直角边为x厘米，依据勾股定理可得，x²+x²=6²，解得x²=18；依据三角形的面积公式可得空白三角形的面积为$\frac{1}{2}$x²=9；再依据扇形的面积公式S=$\frac{n{πr}^{2}}{360}$，已知n=45，代入数据即可求出扇形的面积，最后用扇形的面积减去空白三角形的面积就得到阴影部分的面积．

解答 解：设空白三角形的直角边为x厘米，由题意可得，
x²+x²=6²
   2x²=36
     x²=18，
所以空白三角形的面积为：$\frac{1}{2}$x²
=$\frac{1}{2}$×18
=9（平方厘米），
扇形的面积为：$\frac{45×3.14{×6}^{2}}{360}$
=4.5×3.14
=14.13（平方厘米）；
阴影部分的面积为：14.13-9=5.13（平方厘米．）；
答：阴影部分的面积是5.13平方厘米．

点评 本题考查了不规则图形的面积的求法，通过转化为求规则图形的面积的和差解决即可，关键是牢记有关规则图形的面积公式并能灵活运用．