
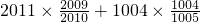
 x-9)×
x-9)× =x-9
=x-9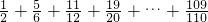
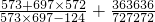
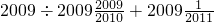
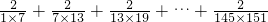 .
. +1004×
+1004× ,
, +(1005-1)×
+(1005-1)× ,
, +
+ +1005×
+1005× -
- ,
,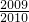 +1004-
+1004-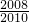 ,
, ,
, ;
; x-9)×
x-9)× =x-9,
=x-9, x-9)×
x-9)× ×5=(x-9)×5,
×5=(x-9)×5, x-9=5x-45,
x-9=5x-45, x-9+9=5x-45+9,
x-9+9=5x-45+9, x=5x-36,
x=5x-36, x-
x- x=5x-36-
x=5x-36- x,
x, x-36=0,
x-36=0, x-36+36=0+36,
x-36+36=0+36, x=36,
x=36, x×
x× =36×
=36× ,
,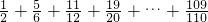 ,
, +1-
+1- +1-
+1- +1-
+1- +…+1-
+…+1- ,
, +
+ +
+ +
+ +…+
+…+ ),
), +
+ -
- +
+ -
- +…+
+…+ -
- ),
), ),
), ,
, ;
;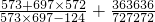 ,
, +
+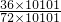 ,
, +
+ ,
, ,
, ;
;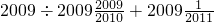 ,
,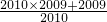 +2009+
+2009+ ,
, +2009+
+2009+ ,
, +
+ +2009,
+2009,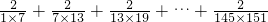 ,
, ×(
×(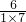 +
+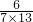 +
+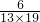 +…+
+…+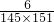 )
) ×(1-
×(1- +
+ -
- +
+ -
-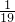 +…
+…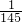 -
- )
) ×(1-
×(1- )
) ×
× ,
,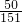 .
. x-9=5x-45,两边同加9,得
x-9=5x-45,两边同加9,得 x=5x-36,两边同减去
x=5x-36,两边同减去 x,得4
x,得4 x-36=0,两边同加36,再同乘
x-36=0,两边同加36,再同乘 即可;
即可; +1-
+1- +1-
+1- +1-
+1- +…+1-
+…+1- ,把1加在一起,分数加在一起,每个分数可以拆成两个分数相减的形式,然后通过加减相抵消的方法,求得结果;
,把1加在一起,分数加在一起,每个分数可以拆成两个分数相减的形式,然后通过加减相抵消的方法,求得结果;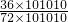 =
= ;
; 写成2009+
写成2009+ ,
, =
= 提出来,原式变为
提出来,原式变为 ×(
×(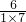 +
+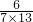 +
+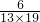 +…+
+…+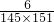 ),然后把括号内的每个分数拆成两个分数相减的形式,通过分数加减相互抵消,得出结果.
),然后把括号内的每个分数拆成两个分数相减的形式,通过分数加减相互抵消,得出结果.

科目:小学数学 来源: 题型:
查看答案和解析>>
科目:小学数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com