解:根据题干分析可得:连接DC.△ADC与△ABC等底等高,所以:S
△ADC=S
△ABC=1,△DCE与△ADC等高,底是其2倍.所以:S
△DCE=2;
连接BE,△BCE与△ABC等高,底是其2倍,所以:S
△BCE=2,△BEF与△BCE等高,底是其的3倍,则其面积也是其的3倍.所以:S
△BEF=2×3=6;
连接AF,△ABF与△ABC等高,底是其的3倍,则面积也是其的3倍.所以:S
△ABF=1×3=3△ADF与△ABF等底等高,则:S
△ADF=3,
所以阴影部分的面积:3+2+6+3+3=17.
答:阴影部分的面积是17.
分析:连接DC.△ADC与△ABC等底等高,所以:S
△ADC=S
△ABC=1,△DCE与△ADC等高,底是其2倍.所以:S
△DCE=2;
连接BE,△BCE与△ABC等高,底是其2倍,所以:S
△BCE=2,△BEF与△BCE等高,底是其的3倍,则其面积也是其的3倍.所以:S
△BEF=2×3=6
连接AF,△ABF与△ABC等高,底是其的3倍,则面积也是其的3倍.所以:S
△ABF=1×3=3△ADF与△ABF等底等高,则:S
△ADF=3,据此加起来即可得出阴影部分的面积.
点评:关键是将阴影部分的面积进行分割,再利用高一定时,三角形的面积与底成正比例的性质,分别求出各个部分的面积即可.

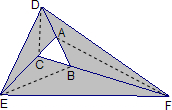
 求阴影部分的面积图形说明:将面积为1的三角形ABC的BA、AC、CB分别延长1倍、2倍、3倍到D、E、F.
求阴影部分的面积图形说明:将面积为1的三角形ABC的BA、AC、CB分别延长1倍、2倍、3倍到D、E、F.


 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
 图形计算.
图形计算.