
【题目】如图, ![]() 是棱形,
是棱形, ![]() 与
与![]() 相交于点
相交于点![]() ,平面
,平面![]() 平面
平面![]() ,且
,且![]() 是直角梯形,
是直角梯形, ![]() .
.

(1)求证: ![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析(2)![]()
【解析】试题分析:(1)由菱形的性质可得![]() ,由线面垂直的性质可得
,由线面垂直的性质可得![]() 平面
平面![]() ,再由线面垂直的性质可得结论;(2)直角梯形
,再由线面垂直的性质可得结论;(2)直角梯形![]() 中,由
中,由![]() 得
得![]() 平面
平面![]() ,取
,取![]() 的中点
的中点![]() ,以
,以![]() 为坐标原点,以
为坐标原点,以![]() 为
为![]() 轴,
轴, ![]() 为
为![]() 轴,
轴, ![]() 为
为![]() 轴,建立空间直角坐标系,分别求出平面
轴,建立空间直角坐标系,分别求出平面![]() 的法向量与平面
的法向量与平面![]() 的法向量,利用空间向量夹角余弦公式可得二面角
的法向量,利用空间向量夹角余弦公式可得二面角![]() 的余弦值.
的余弦值.
试题解析:(1)证明:在棱形![]() 中,可得
中,可得![]() ,
,
因为平面![]() 平面
平面![]() ,且交线为
,且交线为![]() ,
,
所以![]() 平面
平面![]() ,
,
因为![]() 平面
平面![]() ,所以
,所以![]() .
.
(2)直角梯形![]() 中,由
中,由![]() ,得
,得![]() 平面
平面![]() .
.
取![]() 的中点
的中点![]() ,以
,以![]() 为坐标原点,以
为坐标原点,以![]() 为
为![]() 轴,
轴, ![]() 为
为![]() 轴,
轴, ![]() 为
为![]() 轴,建立空间直角坐标系,则
轴,建立空间直角坐标系,则![]() .
.
所以![]() .
.
设平面![]() 的法向量
的法向量![]() ,
,
由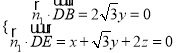 ,可取
,可取![]()
由![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,
,
同上得,可取![]() .
.
则![]() ,
,
即二面角![]() 的余弦值为
的余弦值为![]() .
.
【方法点晴】本题主要考查线面垂直判定与性质以及利用空间向量求二面角的大小,属于难题. 空间向量解答立体几何问题的一般步骤是:(1)观察图形,建立恰当的空间直角坐标系;(2)写出相应点的坐标,求出相应直线的方向向量;(3)设出相应平面的法向量,利用两直线垂直数量积为零列出方程组求出法向量;(4)将空间位置关系转化为向量关系;(5)根据定理结论求出相应的角和距离.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:小学数学 来源: 题型:
【题目】根据运算定律填上合适的字母、图形或数字。
○×(△+☆)=○×________+________×________
102×a=________×a+________×a
53+42=________+________
124+35+76 =(________+________)+35
35×43×4 =(________×________)×________
________×34+________×6=28×(________+________)
(18+26)×5 =18×________+26×________
103+28+97+72=(________+________)+(________+________)
查看答案和解析>>
科目:小学数学 来源: 题型:
【题目】下面是四(1)班同学几项体育项目成绩达标人数统计表。

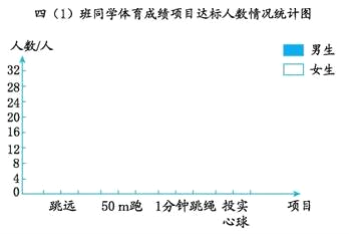
(1)根据以上数据完成复式统计图。
(2)________项目男生达标人数最多,________项目女生达标的人数最多。
(3)全班达标人数最少的项目是________。
(4)这个班至少有________人。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com