
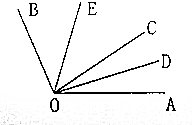
 如图,已知△AOB=112°,射线OC为∠AOB内的一条射线,OD、OE分别平分∠AOC、∠COB.
如图,已知△AOB=112°,射线OC为∠AOB内的一条射线,OD、OE分别平分∠AOC、∠COB.分析 (1)根据角平分线的定义表示出∠COD和∠COE,再根据∠AOB=112°进行计算即可得解.
(2)其它条件都不变,也就是OD、OE分别平分∠AOC、∠COB,∠AOB=112°不变;
根据角平分线的性质可得∠DOC=$\frac{1}{2}$∠AOC,∠COE=$\frac{1}{2}$∠BOC,则∠DOE=∠DOC+∠COE=$\frac{1}{2}$∠AOC+$\frac{1}{2}$∠BOC=$\frac{1}{2}$∠AOB,即可求得结果.
解答 解:(1)因为射线OD和射线OE分别平分∠AOC和∠BOC,
所以∠COD=∠AOD,∠COE=∠BOE,
所以∠DOE=∠COD+∠COE=(∠AOC+∠BOC)×$\frac{1}{2}$=∠AOB×$\frac{1}{2}$
因为∠AOB=112°,
所以∠DOE=112°×$\frac{1}{2}$=56°.
(2)因为OD、OE分别平分∠AOC、∠COB
所以∠DOC=$\frac{1}{2}$∠AOC,∠COE=$\frac{1}{2}$∠BOC
所以∠DOE=∠DOC+∠COE=$\frac{1}{2}$∠AOC+$\frac{1}{2}$∠BOC=$\frac{1}{2}$∠AOB,
所以,∠DOE的大小不会发生变化.
故答案为:56°.
点评 解题的关键是熟练掌握角的平分线把角分成相等的两个小角,且都等于大角的一半,注意本题要有整体意识.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:小学数学 来源: 题型:计算题
查看答案和解析>>
科目:小学数学 来源: 题型:选择题
| A. | 3.14×52×3 | B. | $\frac{1}{3}$×(3.14×5)2×3 | C. | $\frac{1}{3}$×3.14×52×3 |
查看答案和解析>>
科目:小学数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com