
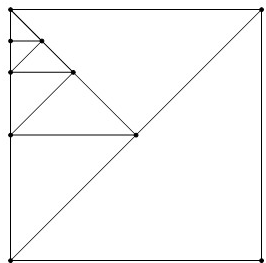
 数字和图形结合.计算:$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{8}$+$\frac{1}{16}$+$\frac{1}{32}$+$\frac{1}{64}$+$\frac{1}{128}$.
数字和图形结合.计算:$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{8}$+$\frac{1}{16}$+$\frac{1}{32}$+$\frac{1}{64}$+$\frac{1}{128}$. 分析 根据图形,正方形的一半是$\frac{1}{2}$,一半的一半是$\frac{1}{4}$,依次$\frac{1}{4}$的一半是$\frac{1}{8}$,…只到平分7次是$\frac{1}{128}$,求$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{8}$+$\frac{1}{16}$+$\frac{1}{32}$+$\frac{1}{64}$+$\frac{1}{128}$根据图形,可以看出再加上$\frac{1}{128}$就是一个正方形,即它们的和就是1-$\frac{1}{128}$,据此得解.
解答 解:根据图形,把正方形看做“1”,则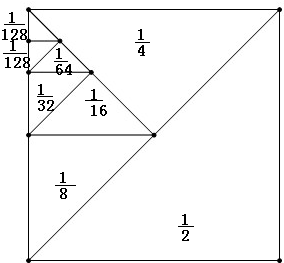
$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{8}$+$\frac{1}{16}$+$\frac{1}{32}$+$\frac{1}{64}$+$\frac{1}{128}$
=1-$\frac{1}{128}$
=$\frac{127}{128}$
点评 灵活运用数形的结合发现规律是解决此题的关键.


科目:小学数学 来源: 题型:解答题
查看答案和解析>>
科目:小学数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com