Question

在如图的立体屋模型中，共有多少条对角线？

Answer 1

考点：排列组合

专题：传统应用题专题

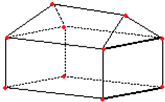
分析：首先确定立体屋模型中共有10个顶点，其中经过四条棱的有4个，经过三条棱的有6个，然后分别求出它们的对角线条数，进而求出立体屋模型中的对角线的条数即可．

解答： 解：如图，立体屋模型中共有10个顶点，其中经过四条棱的有4个，经过三条棱的有6个．
经过四条棱的每一个顶点可以和其余的5个顶点连成5条对角线，所以4个这样的点共可连成5×4=20（条）对角线；
经过三条棱的每一个顶点可以和其余的6个顶点连成6条对角线，所以6个这样的点共可连成6×6=36（条）对角线；
任取两个点A和B，对角线AB和对角线BA算一条，所以立体屋模型中共有（20+36）÷2=28（条）对角线．
答：共有28条对角线．

点评：此题考查了学生排列组合方面的知识，注意分类，注意不能多数、漏数．