
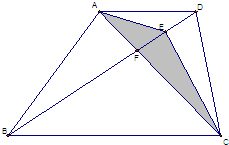
 如图所示,ABCD是梯形,三角形ADE的面积为1,三角形ABF的面积为9,三角形BCF的面积为27,则三角形ACE的面积为
如图所示,ABCD是梯形,三角形ADE的面积为1,三角形ABF的面积为9,三角形BCF的面积为27,则三角形ACE的面积为

科目:小学数学 来源: 题型:
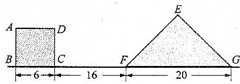 如图所示正方形ABCD与1个等腰直角三角形EFG(EF=EG),放在同一直线上.现在三角形不动,正方形以每秒2厘米的速度向右沿直线匀速运动.试回答以下情况时,正方形与三角形重叠部分的面积是多少?
如图所示正方形ABCD与1个等腰直角三角形EFG(EF=EG),放在同一直线上.现在三角形不动,正方形以每秒2厘米的速度向右沿直线匀速运动.试回答以下情况时,正方形与三角形重叠部分的面积是多少?查看答案和解析>>
科目:小学数学 来源: 题型:
 如图所示,P是长方形ABCD内一点,连接PA、PB、PC、PD,长方形被分成甲、乙、丙、丁四个三角形,已知甲的面积占长方形面积的15%,比丙的面积少30平方厘米,长方形ABCD的面积是多少平方厘米?
如图所示,P是长方形ABCD内一点,连接PA、PB、PC、PD,长方形被分成甲、乙、丙、丁四个三角形,已知甲的面积占长方形面积的15%,比丙的面积少30平方厘米,长方形ABCD的面积是多少平方厘米?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com