
分析 甲乙两队合做12天可以完成,求出甲乙的工作效率之和$\frac{1}{12}$;甲队做2天,乙队做5天,相当于甲乙合作2天,乙再单独做5-2=3天,正好完成这项工程的$\frac{1}{4}$,根据工作量=工作效率×工作时间,求出甲乙合作2天的工作量,进而求出乙单独做3天的工作量,以及乙的工作效率,进一步求得由乙队单独完成,一共需要多少天即可.
解答 解:1÷[($\frac{1}{4}$-$\frac{1}{12}$×2)÷(5-2)]
=1÷[$\frac{1}{12}$÷3]
=1÷$\frac{1}{36}$
=36(天)
答:这项工程由乙单独完成,共需36天.
点评 本题考查了工作时间、工作量、工作效率三者之间的关系.解答本题的关键是先求出乙的工作效率.


 高中必刷题系列答案
高中必刷题系列答案科目:小学数学 来源: 题型:填空题
查看答案和解析>>
科目:小学数学 来源: 题型:选择题
 ,从正面看到的形是
,从正面看到的形是 ,从左面看到的形状是
,从左面看到的形状是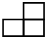 ,这是由( )个小正方体搭成的立体图形.
,这是由( )个小正方体搭成的立体图形.| A. | 4 | B. | 6 | C. | 8 | D. | 9 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com