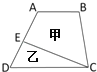
【题目】如图所示，E是AD边上的中点，CE把梯形分成甲、乙两个部分，面积比是10：7，上底AB与下底CD的长度比是 ．
【答案】3：14
【解析】
试题分析：此题先连接AC，S△ACE=S△DEC=7，S△ACD=S△AEC+S△EDC=14，S△ACB=10﹣7=3，又因为S△ACD和S△ACB同高，它们底边的比就是它们面积的比，S△ACB：S△ACD=3：14，所以AB：CD=3：14．
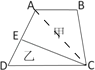
解；S△AEC=S△EDC=7，
S△ACD=S△AEC+S△EDC=7+7=14，
S△ACB=10﹣7=3，
S△ACB：S△ACD=3：14，
S△ACB与S△ACD高相等，面积之比就是它们的底边之比，
即AB与CD长度的比是3：14．
答：AB与CD长度的比是3：14．
故答案为：3：14．
全优点练单元计划系列答案科目：小学数学 来源： 题型：
【题目】按要求凑数
凑6： 1和（_____）
（_____）和3
（_____）和2
凑8： 1和（_____）
5和（_____）
4和（_____）
2和（_____）
凑10：3和（_____）
2和（_____）
5和（_____）
4和（______）
（_______）和5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com