
分析 把这个水池的容量看成单位“1”,那么甲管的工作效率是$\frac{1}{20}$,甲、乙两管的工作效率是$\frac{1}{8}$,根据分数减法的意义,即可求出乙管的工作效率;再根据乙、丙两管的工作效率和是$\frac{1}{6}$,用$\frac{1}{6}$减去乙管的工作效率,就是丙管的工作效率;然后根据关系式:工作量÷工作效率=工作时间,解决问题.
解答 解:1÷[$\frac{1}{6}$-($\frac{1}{8}$-$\frac{1}{20}$)]
=1÷[$\frac{1}{6}$-$\frac{3}{40}$]
=1÷$\frac{11}{120}$
=$\frac{120}{11}$(小时)
答:单开丙管需$\frac{120}{11}$小时注满.
点评 此题主要考查工作时间、工作效率、工作总量三者之间的数量关系:工作量÷工作时间=工作效率,工作量÷工作效率=工作时间.


科目:小学数学 来源: 题型:判断题
查看答案和解析>>
科目:小学数学 来源: 题型:解答题
查看答案和解析>>
科目:小学数学 来源: 题型:解答题
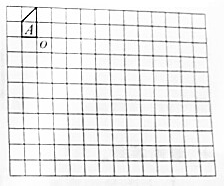 按要求在方格纸上画出图形B、图形C、图形D和图形E.
按要求在方格纸上画出图形B、图形C、图形D和图形E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com